Question

[Tran Tuan Khang]

Giải giúp mình chi tiết nhá

Answer 1

[Yen Nhi]

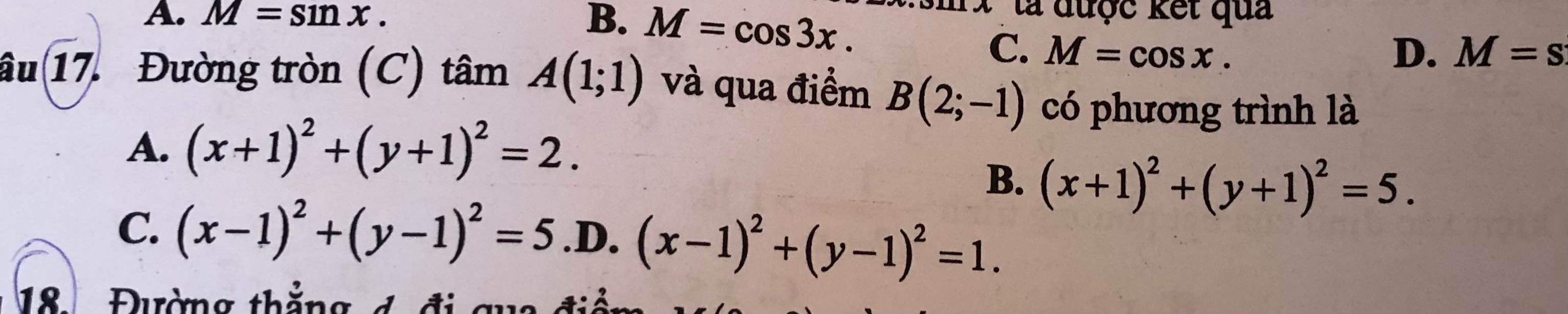
Answer:

Áp dụng bất đẳng thức Bunhiacopxki cho hai cặp số \(\left(1,1\right),\left(\sqrt{a+1},\sqrt{b+1}\right)\)

\(A=1.\sqrt{a+1}+1.\sqrt{b+1}\le\sqrt{\left(1+1\right)\left(a+1+b+1\right)}\) mà \(a+b=1\Rightarrow A\le\sqrt{6}\)

Dấu "=" xảy ra khi: 

\(\sqrt{a+1}=\sqrt{b+1}\)

\(\Leftrightarrow a=b\)

\(\Leftrightarrow a=b=\frac{1}{2}\)

Vậy giá trị lớn nhất của \(A=6\) khi \(a=b=\frac{1}{2}\)