K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

18 tháng 4 2016
S D A H B M C I N
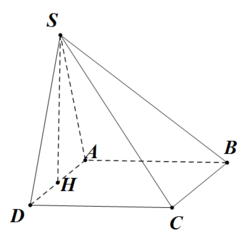
Gọi H là tâm của ABCD\(\Rightarrow SH\perp\left(ABCD\right)\)
M là trung điểm của BC \(\Rightarrow BC\perp\left(SHM\right)\)
Do các mặt bên tạo với đáy cùng 1 góc => \(\widehat{SHM}\) bằng góc tạo bởi 2 mặt bên với đáy
Tính được \(SH=\frac{a\sqrt{3}}{2}'HM=\frac{a}{2}\)
\(\tan\widehat{SMH}=\frac{SH}{MH}=\sqrt{3}\Rightarrow\widehat{SMN}=60^0\)
Lập luận được tâm khối cầu là điểm I của SH với trung trực SC trong (SHC)
Tính được bán kính khối cầu do tam giác SNI đồng dạng với tam giác SHC
\(\Rightarrow SI=\frac{SN.SC}{SH}=\frac{5a}{4\sqrt{3}}\)
Vậy \(V=\frac{4}{3}\pi R^2=\frac{125a^3\sqrt{3}\pi}{432}\)
BJ
1



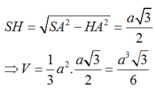

Lời giải:
Đặt $AB=x$. Gọi $O$ là tâm đáy $ABCD$, $T$ là trung điểm $AB$
Ta có:
\(OT=\frac{BC}{2}=\frac{AB}{2}=\frac{x}{2}\) (tính chất đường trung bình)
$T$ là trung điểm $AB$, mà $SAB$ là tam giác đều nên $ST\perp AB$. Áp dụng đl Pitago:
\(ST^2=SB^2-BT^2=AB^2-(\frac{AB}{2})^2=x^2-(\frac{x}{2})^2=\frac{3}{4}x^2\)
Vì $S.ABCD$ là hình chóp đều nên $SO\perp (ABCD)\Rightarrow SO\perp OT$
Áp dụng đl Pitago: \(SO=\sqrt{ST^2-OT^2}=\sqrt{\frac{3}{4}x^2-(\frac{x}{2})^2}=\frac{x}{\sqrt{2}}\)
\(\Rightarrow S_{ABCD}=\frac{1}{3}.SO.S_{ABCD}=\frac{1}{3}.\frac{x}{\sqrt{2}}.x^2=\frac{a^3\sqrt{2}}{6}\)
\(\Rightarrow x=a\)
Vậy $AB=a$