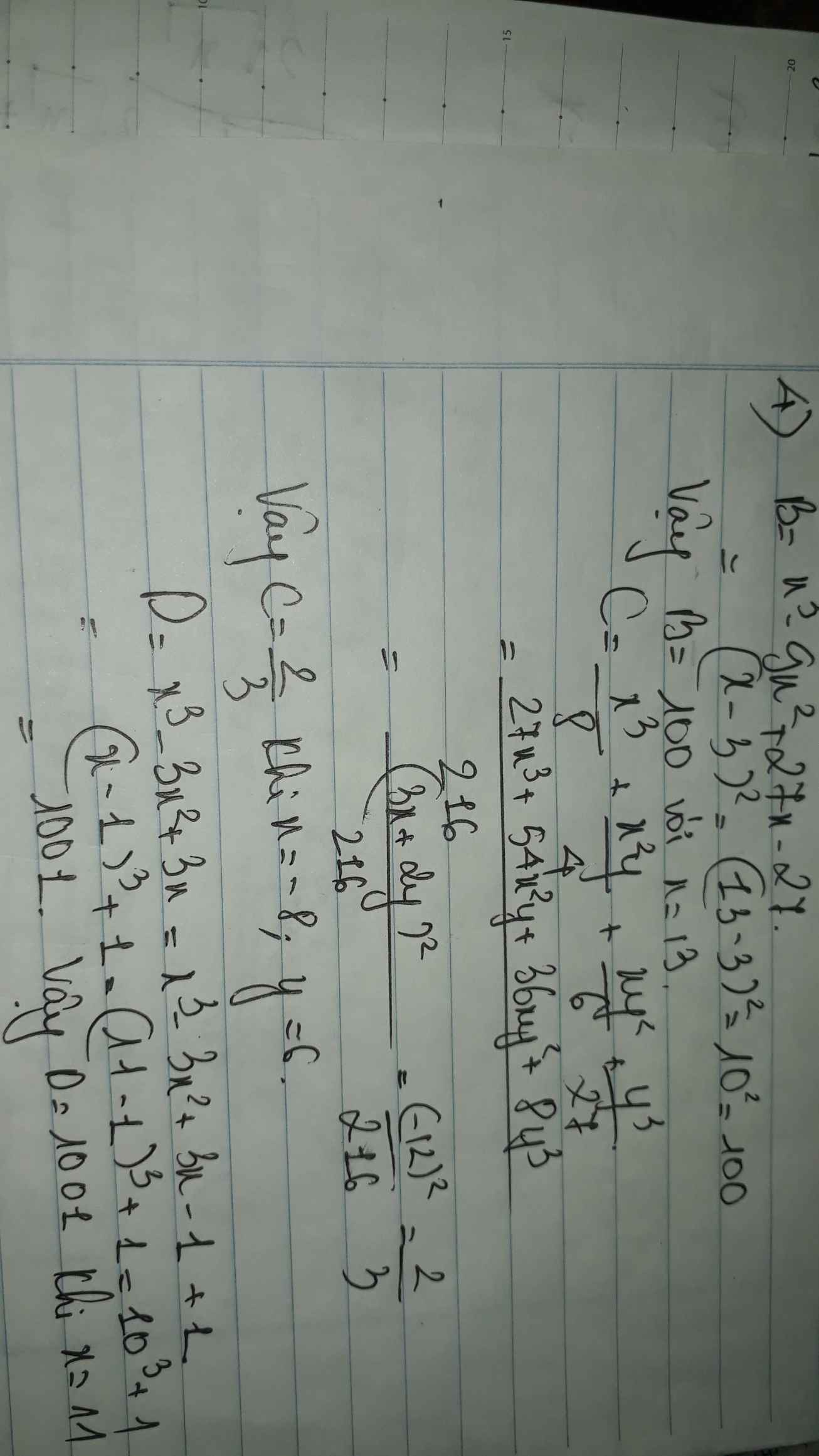Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


c: (x-2)^2+2(2-x)=0
=>(x-2)^2-2(x-2)=0
=>(x-2)(x-4)=0
=>x=2 hoặc x=4
Mọi người giải giúp mình bài này với ạ, cảm ơn mn nhiều, chỉ cần câu c ý chứng minh góc 90 độ thôi ạ

a: Xét tứ giác ABQN có
\(\widehat{BQN}=\widehat{QNA}=\widehat{NAB}=90^0\)
=>ABQN là hình chữ nhật
b: Xét ΔCAD có
DN,CH là các đường cao
DN cắt CH tại M
Do đó: M là trực tâm của ΔCAD
=>AM\(\perp\)CD
c: Xét ΔHAB vuông tại H và ΔHCA vuông tại H có
\(\widehat{HAB}=\widehat{HCA}\left(=90^0-\widehat{ABC}\right)\)
Do đó: ΔHAB đồng dạng với ΔHCA
=>\(\dfrac{HA}{HC}=\dfrac{HB}{HA}\)
=>\(HA^2=HB\cdot HC\)
=>\(HA=\sqrt{HB\cdot HC}\)

\(b,N=\left(2x-1\right)^2-4\ge-4\\ N_{min}=-4\Leftrightarrow x=\dfrac{1}{2}\\ c,P=\left(2x-5\right)^2+6\left(2x-5\right)+9-4\\ P=\left(2x-5+3\right)^2-4=\left(2x-2\right)^2-4\ge-4\\ P_{min}=-4\Leftrightarrow x=1\\ d,Q=\left(x^2-2x+1\right)+\left(y^2+4y+4\right)+1\\ Q=\left(x-1\right)^2+\left(y+2\right)^2+1\ge1\\ Q_{min}=1\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-2\end{matrix}\right.\)
6a.
$M=x^2-x+1=(x^2-x+\frac{1}{4})+\frac{3}{4}$
$=(x-\frac{1}{2})^2+\frac{3}{4}\geq \frac{3}{4}$
Vậy $M_{\min}=\frac{3}{4}$ khi $x-\frac{1}{2}=0\Leftrightarrow x=\frac{1}{2}$

Bài 1:
a: Xét tứ giác BEDF có
ED//BF
ED=BF
Do đó: BEDF là hình bình hành
Suy ra: BE=DF
c: ta có: BEDF là hình bình hành
nên Hai đường chéo EF và BD cắt nhau tại trung điểm của mỗi đường
mà AC và BD cắt nhau tại trung điểm của mỗi đường
nên AC,BD,EF đồng quy

Nếu là câu c
c, Ta có : BD là phân giác \(\widehat{ABC}\)
\(\Rightarrow\dfrac{AD}{DC}=\dfrac{AB}{BC}\left(1\right)\)
Ta có : BK là phân giác \(\widehat{ABH}\)
\(\Rightarrow\dfrac{HK}{AK}=\dfrac{BH}{AB}\left(2\right)\)
Ta có: ΔHBA ~ ΔABC (cmt )
(*nếu chưa c/m tam giác đồng dạng thì hãy c/m, làm r thì khỏi )
\(\Rightarrow\dfrac{HB}{AB}=\dfrac{AB}{AC}\left(3\right)\)
\(\left(1\right)\left(2\right)\left(3\right)\Rightarrow\dfrac{AD}{DC}=\dfrac{HK}{AK}\)
\(\Rightarrow AK.AD=HK.CD\left(đpcm\right)\)


c: ĐKXĐ: x<>8
\(\dfrac{3}{2x-16}+\dfrac{3x-20}{x-8}+\dfrac{1}{8}=\dfrac{13x-102}{3x-24}\)
=>\(\dfrac{9}{6\left(x-8\right)}+\dfrac{18x-120}{6\left(x-8\right)}-\dfrac{26x-204}{6\left(x-8\right)}=\dfrac{-1}{8}\)
=>\(\dfrac{18x-111-26x+204}{6\left(x-8\right)}=\dfrac{-1}{8}\)
=>\(\dfrac{-8x+93}{6x-48}=\dfrac{-1}{8}\)
=>\(\dfrac{8x-93}{6x-48}=\dfrac{1}{8}\)
=>8(8x-93)=6x-48
=>64x-744-6x+48=0
=>58x=696
=>x=12
d: ĐKXĐ: x<>1; x<>-1
\(\dfrac{6}{x^2-1}+5=\dfrac{8x-1}{4x+4}+\dfrac{12x-1}{4x-4}\)
=>\(\dfrac{24}{4\left(x-1\right)\left(x+1\right)}+\dfrac{20\left(x^2-1\right)}{4\left(x-1\right)\left(x+1\right)}=\dfrac{\left(8x-1\right)\left(x-1\right)+\left(12x-1\right)\left(x+1\right)}{4\left(x-1\right)\left(x+1\right)}\)
=>8x^2-9x+1+12x^2+12x-x-1=24+20x^2-20
=>20x^2+2x=20x^2+4
=>2x=4
=>x=2(loại)


Bài 4:
c) Ta có: \(\dfrac{x^3}{8}+\dfrac{x^2y}{2}+\dfrac{xy^2}{6}+\dfrac{y^3}{27}\)
\(=\left(\dfrac{x}{2}\right)^3+3\cdot\left(\dfrac{x}{2}\right)^2\cdot\dfrac{y}{3}+3\cdot\dfrac{x}{2}\cdot\left(\dfrac{y}{3}\right)^2+\left(\dfrac{y}{3}\right)^3\)
\(=\left(\dfrac{1}{2}x+\dfrac{1}{3}y\right)^3\)
\(=\left(\dfrac{-1}{2}\cdot8+\dfrac{1}{3}\cdot6\right)^3=\left(-4+2\right)^3=-8\)

1a.
\(2x^2+7xy+5y^2-5y-2x\)
\(=2x^2+5xy+2xy+5y^2-5y-2x\)
\(=x\left(2x+5y\right)+y\left(2x+5y\right)-\left(2x+5y\right)\)
\(=\left(2x+5y\right)\left(x+y-1\right)\)

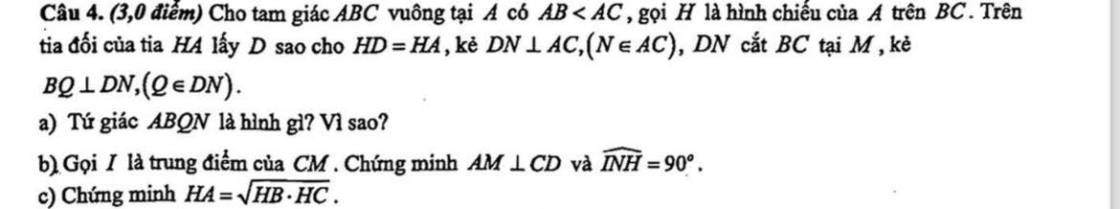
 giải giúp mình câu c với ạ, mình cảm ơnnnnn
giải giúp mình câu c với ạ, mình cảm ơnnnnn giải giúp mình câu b, c với ạ!
giải giúp mình câu b, c với ạ!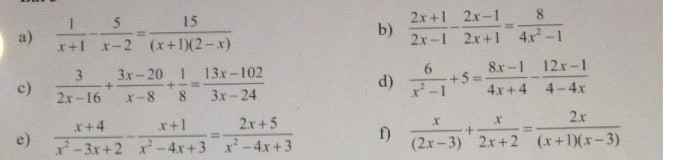

 giúp mình bài 4 câu B,C D với ạ
giúp mình bài 4 câu B,C D với ạ