K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
DH
1
23 tháng 9 2021
Xét tam giác ABH vuông tại H có:
\(sinB=\dfrac{AH}{AB}=0,5\Rightarrow AB=\dfrac{AH}{0,5}=\dfrac{5}{0,5}=10\)
Xét tam giác ABH vuông tại H có:
\(AB^2=AH^2+BH^2\left(Pytago\right)\)
\(\Rightarrow BH=\sqrt{AB^2-AH^2}=\sqrt{10^2-5^2}=5\sqrt{3}\)
DH
0
ML
0
7 tháng 9 2021
a: ĐKXĐ: \(x\ge1\)
b: ĐKXĐ: \(x\ge-2\)
c: ĐKXĐ: \(x\le-2\)
d: ĐKXĐ: \(x\le0\)
14 tháng 10 2021
bạn tự vẽ hình giúp mik nha
a.ta có \(\Delta\)ABC nội tiếp (O) và AB là đường kính nên \(\Delta\)ABC vuông tại C
trong \(\Delta ABC\) vuông tại C có
AC=AB.cosBAC=10.cos30=8,7
BC=AB.sinCAB=10.sin30=5
ta có Bx là tiếp tuyến của (O) nên Bx vuông góc với AB tại B
trong \(\Delta\)ABE vuông tại B có
\(cosBAE=\dfrac{AB}{AE}\Rightarrow AE=\dfrac{AB}{cosBAE}=\dfrac{10}{cos30}=11,5\)
mà:CE=AE-AC=11,5-8,7=2,8
b.áp dụng pytago vào \(\Delta ABE\) vuông tại B có
\(BE=\sqrt{AE^2-AB^2}=\sqrt{11,5^2-10^2}=5,7\)
13 tháng 3 2023
15:
a: \(\text{Δ}=\left(m^2-m+2\right)^2-4m^2\)
=(m^2-m+2-2m)(m^2-m+2+2m)
=(m^2+m+2)(m^2-3m+2)
=(m-1)(m-2)(m^2+m+2)
Để phương trình co hai nghiệm phân biệt thì (m-1)(m-2)(m^2+m+2)>0
=>(m-1)(m-2)>0
=>m>2 hoặc m<1
b: x1+x2=m^2-m+2>0 với mọi m
x1*x2=m^2>0 vơi mọi m
=>Phương trình luôn có hai nghiệm dương phân biệt
3 tháng 9 2021
b: Xét ΔABE vuông tại A có AH là đường cao ứng với cạnh huyền BE
nên \(BH\cdot BE=AB^2\left(1\right)\)
Xét ΔABC vuông tại B có BH là đường cao ứng với cạnh huyền AC
nên \(AH\cdot AC=AB^2\left(2\right)\)
Từ (1) và (2) suy ra \(BH\cdot BE=AH\cdot AC\)
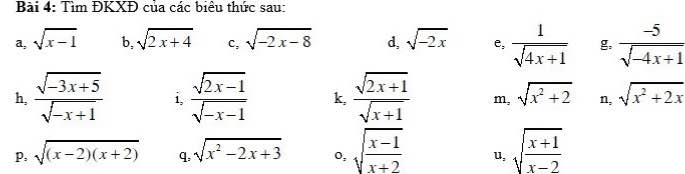
Kẻ \(AH\perp BC\)
Có \(sinB=\dfrac{AH}{AB}\)
\(\Rightarrow AB.sinB=AH\)\(\Leftrightarrow\dfrac{1}{2}AB.BC.sinB=\dfrac{1}{2}AH.BC=S_{ABC}\)
Có \(sinC=\dfrac{AH}{AC}\)
\(\Rightarrow AC.sinC=AH\)\(\Leftrightarrow\dfrac{1}{2}AC.BC.sinC=\dfrac{1}{2}AH.BC=S_{ABC}\)
\(\Rightarrow\dfrac{1}{2}AB.BC.sinB=\dfrac{1}{2}AC.BC.sinC=S_{ABC}\)
Áp dụng \(S_{ABC}=\dfrac{1}{2}AB.BC.sinB=\dfrac{1}{2}.10.15.sin60^0=\dfrac{75\sqrt{3}}{2}\left(cm^2\right)\)
Kẻ đường cao AH của tam giác ABC
Áp dụng tslg trong tam giác ABH vuông tại H và tam giác AHC vuông tại H:
\(sinB=\dfrac{AH}{AB},sinC=\dfrac{AH}{AC}\)
\(S_{ABC}=\dfrac{1}{2}BC.AH=\dfrac{1}{2}AB.BC.\dfrac{AH}{AB}=\dfrac{1}{2}AB.BC.sinB\)
\(S_{ABC}=\dfrac{1}{2}BC.AH=\dfrac{1}{2}AC.BC.\dfrac{AH}{AC}=\dfrac{1}{2}AC.BC.sinC\)
\(S_{ABC}=\dfrac{1}{2}AB.BC.sinB=\dfrac{1}{2}.10.15.sin60^0=\dfrac{1}{2}.10.15.\dfrac{\sqrt{3}}{2}=\dfrac{75\sqrt{3}}{2}\left(cm^2\right)\)