
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có: \(3x=4y\Rightarrow\dfrac{x}{4}=\dfrac{y}{3}\Rightarrow\dfrac{x}{20}=\dfrac{y}{15}\)
\(2y=5z\Rightarrow\dfrac{y}{5}=\dfrac{z}{2}\Rightarrow\dfrac{y}{15}=\dfrac{z}{6}\)
Áp dụng t/c dtsbn:
\(\dfrac{x}{20}=\dfrac{y}{15}=\dfrac{z}{6}=\dfrac{x+z}{20+6}=\dfrac{52}{26}=2\)
\(\Rightarrow\left\{{}\begin{matrix}x=20.2=40\\y=15.2=30\\z=6.2=12\end{matrix}\right.\)

Áp dụng tc dãy tỉ:
\(\frac{x}{7}=\frac{y}{13}=\frac{x+y}{7+13}=\frac{40}{20}=2\)
\(\Rightarrow\begin{cases}\frac{x}{7}=2\Rightarrow x=14\\\frac{y}{13}=2\Rightarrow y=26\end{cases}\)
\(\frac{x}{7}=\frac{y}{13}\) và x+y=40
\(\frac{x}{7}=\frac{y}{13}=\frac{x+y}{7+13}=\frac{40}{20}=2\)
=>x=14
y=36
vậy x=14
y=36
mai anh em ta gặp nhau có gì k hiểu hỏi anh nhé

\(\left(\frac{2}{7}\right)^{2008}:\left(\frac{4}{49}\right)^{1004}\)
\(=\left(\frac{2}{7}\right)^{2008}:\left[\left(\frac{2}{7}\right)^2\right]^{1004}\)
\(=\left(\frac{2}{7}\right)^{2008}:\left(\frac{2}{7}\right)^{2008}\)
= 1
Học tốt
#Gấu

a/ Tam giác AMN cân tại A (gt). \(\Rightarrow\) \(\widehat{AMN}=\widehat{ANM};AM=AN.\)
Xét tam giác AMB và tam giác ANC có:
+ AM = AN (cmt).
+ \(\widehat{AMB}=\widehat{ANC}\left(\widehat{AMN}=\widehat{ANM}\right).\)
+ MB = NC (gt).
\(\Rightarrow\) Tam giác AMB = Tam giác ANC (c - g - c).
\(\Rightarrow\) AB = AC (cặp cạnh tương ứng).
Xét tam giác ABC có: AB = AC (cmt).
\(\Rightarrow\) Tam giác ABC cân tại A.
b/ Tam giác ABC cân tại A (cmt) \(\Rightarrow\) \(\widehat{ABC}=\widehat{ACB}.\)
Mà \(\widehat{ABC}=\widehat{MBH;}\widehat{ACB}=\widehat{NCK}\text{}\) (đối đỉnh).
\(\Rightarrow\) \(\widehat{MBH}=\widehat{NCK}.\)
Xét tam giác MBH và tam giác NCK \(\left(\widehat{BHM}=\widehat{CKN}=90^o\right)\)có:
+ MB = NC (gt).
+ \(\widehat{MBH}=\widehat{NCK}\left(cmt\right).\)
\(\Rightarrow\) Tam giác MBH = Tam giác NCK (cạnh huyền - góc nhọn).
c/ Tam giác MBH = Tam giác NCK (cmt).
\(\Rightarrow\) \(\widehat{BMH}=\widehat{CNK}\) (cặp góc tương ứng).
Xét tam giác OMN có: \(\widehat{NMO}=\widehat{MNO}\) (do \(\widehat{BMH}=\widehat{CNK}\)).
\(\Rightarrow\) Tam giác OMN tại O.

Bài 1:
a: Ta có: \(3\left(x-\dfrac{1}{2}\right)-3\left(x-\dfrac{1}{3}\right)=x\)
\(\Leftrightarrow x=3x-\dfrac{3}{2}-3x+1\)
\(\Leftrightarrow x=-\dfrac{1}{2}\)
b: Ta có: \(-\dfrac{4}{3}\left(x-\dfrac{1}{4}\right)=\dfrac{3}{2}\left(2x-1\right)\)
\(\Leftrightarrow x\cdot\dfrac{-4}{3}+\dfrac{1}{3}-3x+\dfrac{3}{2}=0\)
\(\Leftrightarrow x\cdot\dfrac{-13}{3}=-\dfrac{11}{6}\)
hay \(x=\dfrac{11}{26}\)

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{4}=\dfrac{d}{5}=\dfrac{a+b+c+d}{2+3+4+5}=\dfrac{140}{14}=10\)
Do đó: a=20; b=30; c=40; d=50


a.Xét tam giác vuông AED và tam giác vuông AFD, có:
A: góc chung
AD: cạnh chung
Vậy tam giác vuông AED = tam giác vuông AFD ( cạnh huyền . góc nhọn)
=> DE = DF ( 2 cạnh tương ứng )
b.Xét tam giác vuông BDE và tam giác vuông CDF, có:
góc B = góc C ( gt )
DE = DF ( cmt )
Vậy tam giác vuông BDE = tam giác vuông CDF ( góc nhọn. cạnh góc vuông )
c. ta có: AD là đường phân giác trong tam giác cân ABC cũng là đường trung trực
=> AD là đường trung trực của BC
Chúc bạn học tốt!!!

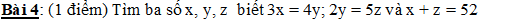

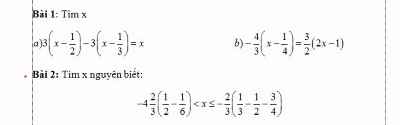 giúp mik giải 2 bài này vs ạ
giúp mik giải 2 bài này vs ạ

