
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




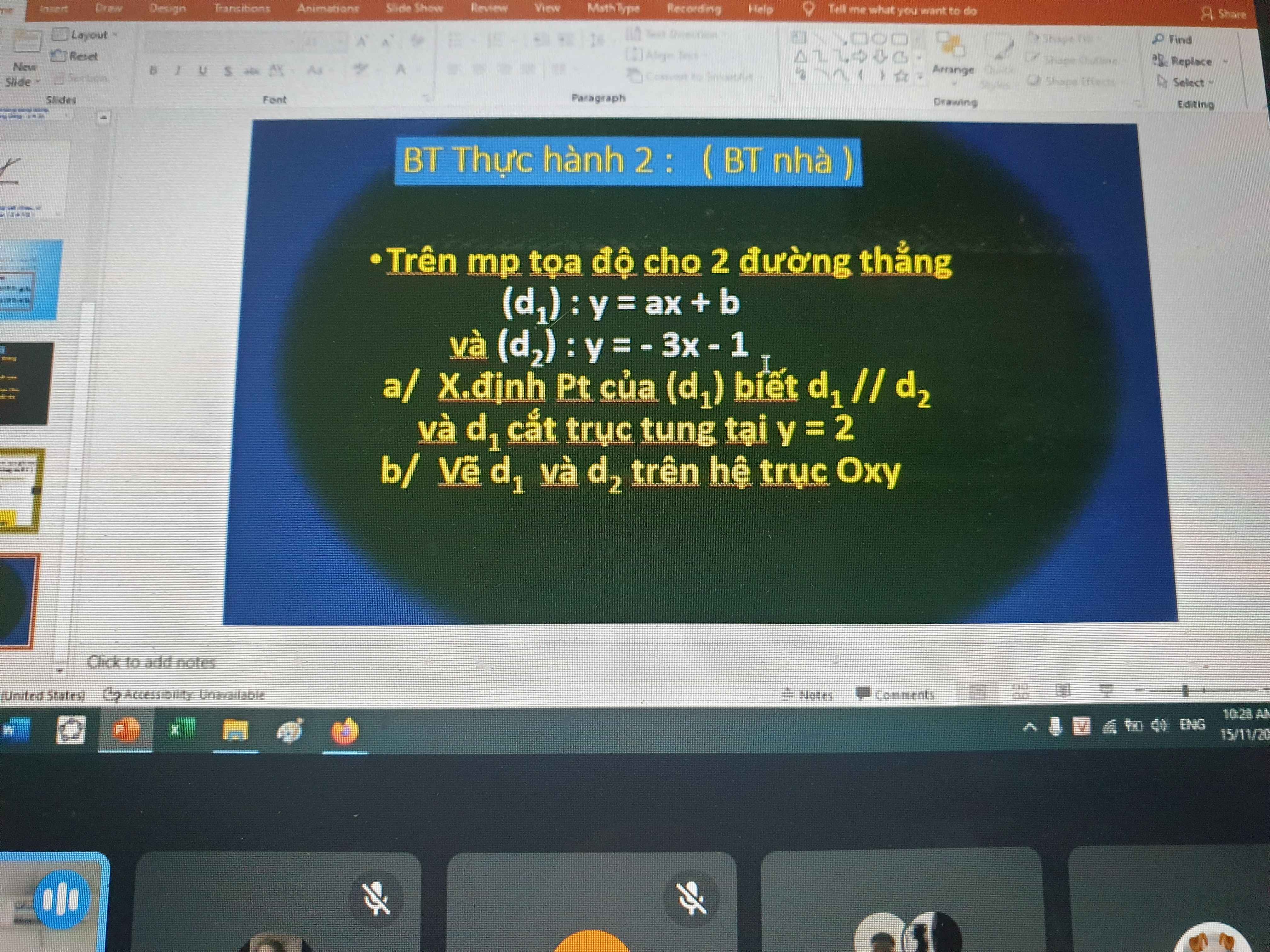
a: Vì (d1)//(d2) nên a=-3
Vậy: (d1): y=-3x+b
Thay x=0 và y=2 vào (d1), ta được:
b=2

a)Hs luon nghịch biến <=> a<0
<=>m-2<0
=>m<2
Vậy với m<2 thì hs đã cho luôn nb
b)Ta có hoành độ gđ giữa d1 và d2
-x+2=2x-1
<=>-3x=-3
=>x=1
Với x=1=>y=1 =>A(1,1)
Để 3 đg thẳng đã cho đồng qui thì A(1,1) phải thuộc (d) y=(m-2)x+3m+3
<=>1=m-2+3m+3
<=>4m=0
=>m=0
Do học năm ngoái nên k nhớ cách trình bày lắm. Sr bạn -.-

Lời giải:
Theo định lý Viet đảo:
a.
$a,b$ là nghiệm của pt:
$x^2-5x+6=0$
$\Leftrightarrow (x-2)(x-3)=0$
$\Leftrightarrow x-2=0$ hoặc $x-3=0$
$\Leftrightarrow x=2$ hoặc $x=3$
Vậy $(a,b)=(2,3), (3,2)$
b. Tương tự:
$a,b$ là nghiệm của pt $x^2-7x+12=0$
c. $a,b$ là nghiệm của pt $x^2-5x-14=0$

\(M=\left(4x^2-4x+1\right)+\left(x+\dfrac{1}{4x}-1\right)+2020\)
\(M=\left(2x-1\right)^2+\dfrac{\left(2x-1\right)^2}{4x}+2020\ge2020\)
\(M_{min}=2020\) khi \(x=\dfrac{1}{2}\)

1:
a: Khi m=-2 thì phương trình sẽ trở thành:
\(x^2+2x-2-1=0\)
=>\(x^2+2x-3=0\)
=>(x+3)(x-1)=0
=>\(\left[{}\begin{matrix}x+3=0\\x-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=1\end{matrix}\right.\)
b: \(x^2+2x+m-1=0\)
\(\text{Δ}=2^2-4\left(m-1\right)=4-4m+4=-4m+8\)
Để phương trình có hai nghiệm thì -4m+8>=0
=>-4m>=-8
=>m<=2
Theo Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-2\\x_1\cdot x_2=m-1\end{matrix}\right.\)
mà \(x_1+2x_2=1\)
nên ta có hệ phương trình:
\(\left\{{}\begin{matrix}x_1+x_2=-2\\x_1+2x_2=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-x_2=-3\\x_1+x_2=-2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x_2=3\\x_1=-2-x_2=-2-3=-5\end{matrix}\right.\)
\(x_1\cdot x_2=m-1\)
=>\(m-1=3\cdot\left(-5\right)=-15\)
=>m=-15+1=-14

a) \(\widehat{AED}=\widehat{AFD}=90^o\) nên \(E,F\) cùng nhìn \(AD\) dưới góc vuông suy ra \(AEDF\) nội tiếp.
suy ra \(\widehat{AEF}=\widehat{ADF}\).
mà \(\widehat{ADF}=\widehat{ACD}\) (vì cùng phụ với góc \(\widehat{DAC}\))
suy ra \(\widehat{AEF}=\widehat{ACD}\Rightarrow\widehat{BEF}+\widehat{FCB}=180^o\) suy ra \(BEFC\) nội tiếp.
b) \(\Delta GBE\sim\Delta GFC\left(g.g\right)\)
suy ra \(GB.GC=GE.GF\).
\(\Delta GDE\sim\Delta GFD\left(g.g\right)\)
suy ra \(GD^2=GE.GF\).
\(ACBH\) nội tiếp suy ra \(GB.GC=GH.GA\)
suy ra \(GD^2=GH.GA\)
\(\Rightarrow\Delta GHD\sim\Delta GDA\left(c.g.c\right)\)
\(\Rightarrow\widehat{GHD}=\widehat{GDA}=90^o\)
suy ra \(DH\) vuông góc với \(AG\).


 Giúp em giải bài này với em đang cần gấp
Giúp em giải bài này với em đang cần gấp

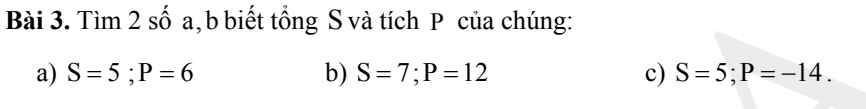

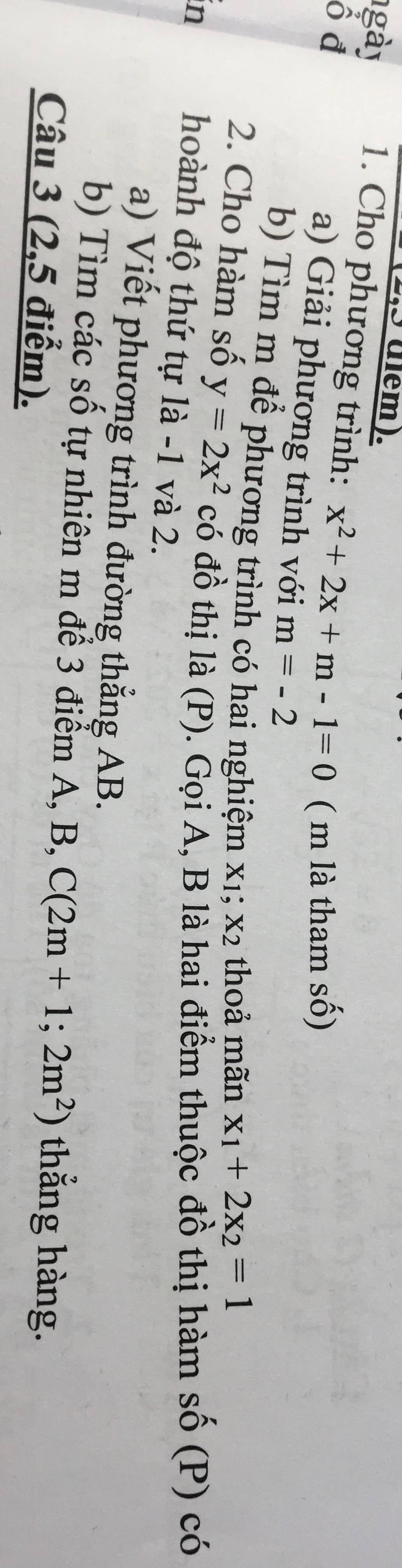
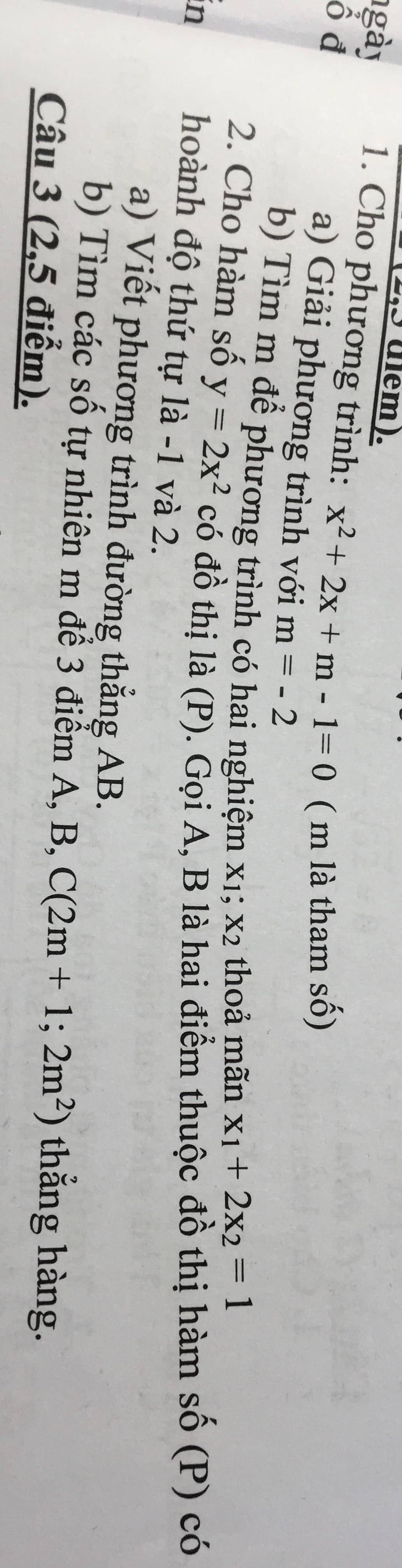
 Giúp em giải bài tập này với ạ. Em cảm ơn.
Giúp em giải bài tập này với ạ. Em cảm ơn.
Lời giải:
$\Delta'=m^2-(4m-3)=m^2-4m+3$
a. Để pt có nghiệm kép thì $\Delta'=0$
$\Leftrightarrow m^2-4m+3=0$
$\Leftrightarrow (m-1)(m-3)=0$
$\Leftrightarrow m=1$ hoặc $m=3$
b. Để pt có 1 nghiệm bằng $4$ thì:
$4^2-2m.4+4m-3=0$
$\Leftrightarrow 13-4m=0$
$\Leftrightarrow m=\frac{13}{4}$
Dạ em cảm ơn ạ