Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cô hướng dẫn nhé. Do tính chất đối xứng, ta suy ra AB = BD; AM = MI hay BM là đường trung bình tam giác ADI.
Từ đó ta có BM // DI và DI = 2BM.
Hoàn toàn tương tự : MC // IE và IE = 2MC
Lại có MB = MC và B, M, C thẳng hàng nên D, I, E thẳng hàng và DI = IE
Vậy D đối xứng với E qua I.

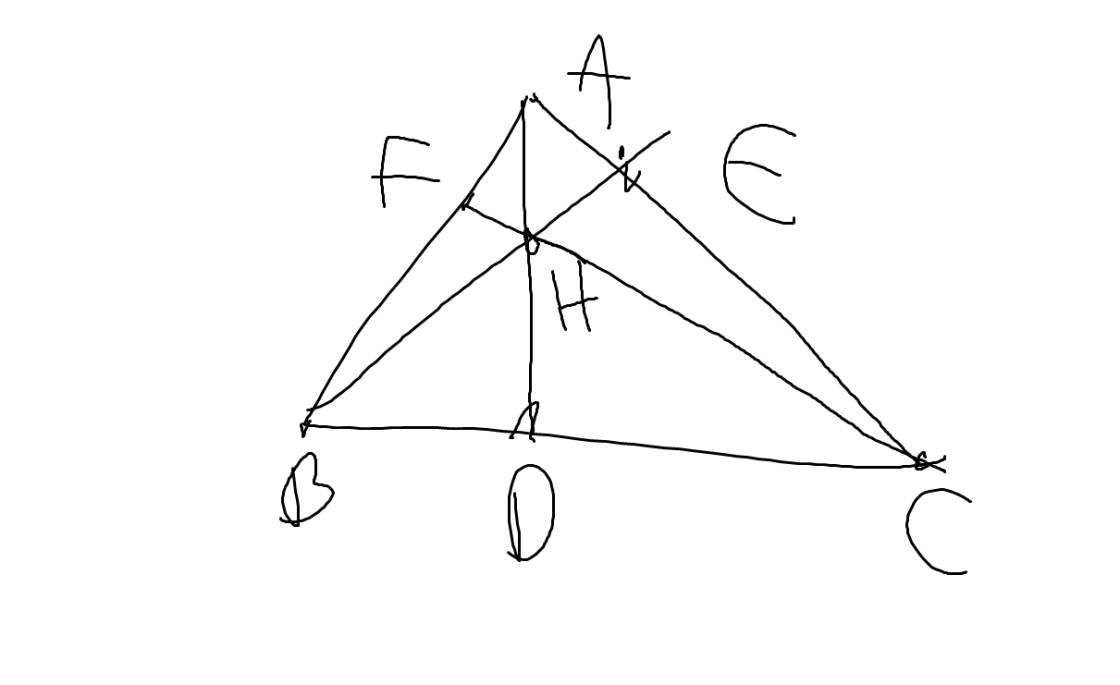
1: Xét tứ giác AFDC có
\(\widehat{AFC}=\widehat{ADC}=90^0\)
nên AFDC là tứ giác nội tiếp
2: Xét tứ giác AEDB có
\(\widehat{AEB}=\widehat{ADB}=90^0\)
nên AEDB là tứ giác nội tiếp
3:
Xét tứ giác AFHE có
\(\widehat{AFH}+\widehat{AEH}=90^0+90^0=180^0\)
=>AEHF là tứ giác nội tiếp
4: Xét tứ giác HECD có
\(\widehat{HEC}+\widehat{HDC}=90^0+90^0=180^0\)
=>HECD là tứ giác nội tiếp


a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)

\(a+b\ge2\sqrt{ab},b+c\ge2\sqrt{bc},c+d\ge2\sqrt{cd},d+e\ge2\sqrt{de},\)
\(e+f\ge2\sqrt{ef},f+a\ge2\sqrt{fa}\)
Suy ra \(\left(a+b\right)\left(b+c\right)\left(c+d\right)\left(d+e\right)\left(e+f\right)\left(f+a\right)\ge2^6\sqrt{a^2b^2c^2d^2e^2f^2}=64\).
Dấu \(=\)xảy ra khi \(a=b=c=d=e=f=1\).

B A F N D M C E
Cô hướng dẫn em câu d nhé, theo cô thấy thì đề của em không đúng, góc vuông ở đây là BND nhé ^^
Do F đối xứng với E qua A nên tam giác BEF cân tại B, từ đó góc FBA = góc ABE. Lại do câu b, góc ABE = góc AMD nên góc NBD bằng góc NMD. Vậy tứ giác BMDN nội tiếp.
Ta thấy góc BMD vuông nên BD là đường kính. Từ đó góc DNB vuông (đpcm)
Chúc em học tốt :))))

?
=37. cộng cái đầu cái cuối
SAO KO AI BIẾT HẢ