Gi
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
Giải giúp bài 1 2 3 4 của bài 15 i
27 tháng 6 2021
`1)1/(1-sqrt2)-1/(1+sqrt2)=(1+sqrt2)/(1-2)-(sqrt2-1)/(2-1)=-(1+sqrt2)-sqrt2+1=-2sqrt2` $\\$ `2)1/(1+sqrt5)+1/(sqrt5-1)=(sqrt5-1)/(5-1)+(sqrt5+1)/(5-1)=(sqrt5-1+sqrt5+1)/4=sqrt5/2` $\\$ `3)4/(1-sqrt3)+(sqrt3-1)/(sqrt3+1)=(4(sqrt3+1))/(1-3)+(sqrt3-1)^2/(3-1)=(-4(sqrt3+1)+4-2sqrt3)/2=-3sqrt3` $\\$ `4)(2-sqrt5)/(2+sqrt5)+(sqrt5+2)/(sqrt5-2)=(2-sqrt5)^2/(4-5)+(sqrt5+2)^2/(5-4)=-(2-sqrt5)^2+(sqrt5+2)^2=9+4sqrt5-9+4sqrt5=8sqrt5`
27 tháng 6 2021
18) Ta có: \(\dfrac{2-\sqrt{2}}{1-\sqrt{2}}+\dfrac{\sqrt{2}-\sqrt{6}}{\sqrt{3}-1}\)
\(=\dfrac{-\sqrt{2}\left(1-\sqrt{2}\right)}{1-\sqrt{2}}+\dfrac{\sqrt{2}\left(1-\sqrt{3}\right)}{-\left(1-\sqrt{3}\right)}\)
\(=-2\sqrt{2}\)
22 tháng 11 2023
Bài 1:
3: ĐKXĐ: x>=1
\(x-\sqrt{x+3+4\sqrt{x-1}}=1\)
=>\(x-\sqrt{x-1+2\cdot\sqrt{x-1}\cdot2+4}=1\)
=>\(x-\sqrt{\left(\sqrt{x-1}+2\right)^2}=1\)
=>\(x-\left|\sqrt{x-1}+2\right|=1\)
=>\(x-\left(\sqrt{x-1}+2\right)=1\)
=>\(x-\sqrt{x-1}-2-1=0\)
=>\(x-1-\sqrt{x-1}-2=0\)
=>\(\left(\sqrt{x-1}\right)^2-2\sqrt{x-1}+\sqrt{x-1}-2=0\)
=>\(\left(\sqrt{x-1}-2\right)\left(\sqrt{x-1}+1\right)=0\)
=>\(\sqrt{x-1}-2=0\)
=>\(\sqrt{x-1}=2\)
=>x-1=4
=>x=5(nhận)
giải giúp mik bài 3 nha mn <3
25 tháng 10 2023
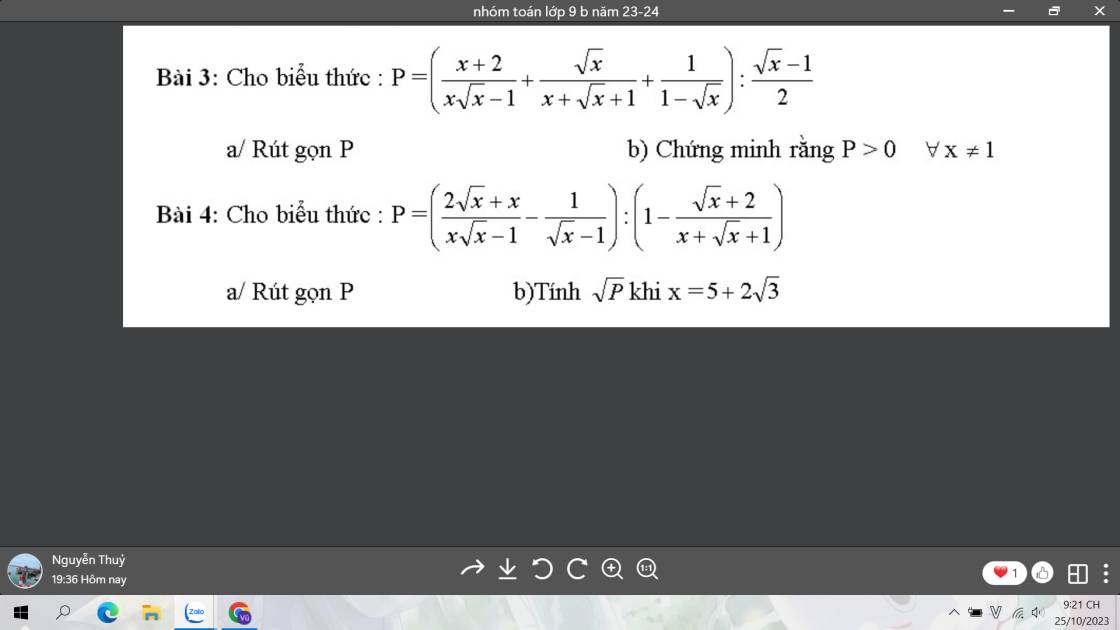
3:
ĐKXĐ: x>=0; x<>1
a: \(P=\left(\dfrac{x+2}{x\sqrt{x}-1}+\dfrac{\sqrt{x}}{x+\sqrt{x}+1}+\dfrac{1}{1-\sqrt{x}}\right):\dfrac{\sqrt{x}-1}{2}\)
\(=\left(\dfrac{x+2}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}+\dfrac{\sqrt{x}}{x+\sqrt{x}+1}-\dfrac{1}{\sqrt{x}-1}\right)\cdot\dfrac{2}{\sqrt{x}-1}\)
\(=\dfrac{x+2+x-\sqrt{x}-x-\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\cdot\dfrac{2}{\sqrt{x}-1}\)
\(=\dfrac{x-2\sqrt{x}+1}{\left(\sqrt{x}-1\right)^2}\cdot\dfrac{2}{x+\sqrt{x}+1}=\dfrac{2}{x+\sqrt{x}+1}\)
b: \(x+\sqrt{x}+1=\sqrt{x}\left(\sqrt{x}+1\right)+1>=0+1=1\)
=>\(x+\sqrt{x}+1>0\forall x\) thỏa mãn ĐKXĐ
mà 2>0
nên \(P=\dfrac{2}{x+\sqrt{x}+1}>0\forall x\) thỏa mãn ĐKXĐ
Y
19 tháng 6 2023
\(53,\sqrt{\left(a-2b\right)^2}\left(a\le2b\right)\)
\(=\left|a-2b\right|=-a+2b\)
\(54,\sqrt{4x^2-4xy+y^2}\left(2x\ge y\right)\)
\(=\sqrt{\left(2x-y\right)^2}=\left|2x-y\right|=2x-y\)
\(55,\sqrt{\left(2x-1\right)^2}\left(x\ge\dfrac{1}{2}\right)\)
\(=\left|2x-1\right|=2x-1\)
\(56,\sqrt{\left(3a-2\right)^2}\left(3a\le2\right)\)
\(=\left|3a-2\right|=-3a+2\)
\(57,\sqrt{\left(6-9x\right)^2}\left(3x\ge2\right)\)
\(=\left|6-9x\right|=-6+9x\)
\(58,\sqrt{25a^2-10a+1}\left(5a\le1\right)\)
\(=\sqrt{\left(5a-1\right)^2}=\left|5a-1\right|=-5a+1\)
\(59,\sqrt{m^2+4mn+4n^2}\left(m\ge-2n\right)\)
\(=\sqrt{\left(m+2n\right)^2}=\left|m+2n\right|=m+2n\)
\(60,\sqrt{9x^2-24xy+16y^2}\left(3x\le4y\right)\)
\(=\sqrt{\left(3x-4y\right)^2}=\left|3x-4y\right|=-3x+4y\)
H9
HT.Phong (9A5)
CTVHS
19 tháng 6 2023
Bài 3:
53. \(\sqrt{\left(a-2b\right)^2}=\left|a-2b\right|=2b-a\)
54. \(\sqrt{4x^2-4xy+y^2}=\sqrt{\left(2x-y\right)^2}=\left|2x-y\right|=2x-y\)
55. \(\sqrt{\left(2x-1\right)^2}=\left|2x-1\right|=2x-1\)
56. \(\sqrt{\left(3a-2\right)^2}=\left|3a-2\right|=2-3a\)
57. \(\sqrt{\left(6-9x\right)^2}=\left|6-9x\right|=6-9x\)
58. \(\sqrt{25a^2-10a+1}=\sqrt{\left(5a-1\right)^2}=\left|5a-1\right|=1-5a\)
59. \(\sqrt{m^2+4mn+4n^2}=\sqrt{\left(m+2n\right)^2}=\left|m+2n\right|=m+2n\)
60. \(\sqrt{9x^2-24xy+16y^2}=\sqrt{\left(3x-4y\right)^2}=\left|3x-4y\right|=4y-3x\)
18 tháng 7 2023
3, ta có:
\(B=\dfrac{\sqrt{x}-3+2\sqrt{x}}{\left(\sqrt{x}+3\right)\left(\sqrt{x-3}\right)}\cdot\dfrac{2\left(\sqrt{x}+3\right)}{\sqrt{x}-1}\\ =\dfrac{3\left(\sqrt{x}-1\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\cdot\dfrac{2\left(\sqrt{x}+3\right)}{\sqrt{x}-1}\\ =\dfrac{6}{\sqrt{x}-3}\)
để B=3 thì ta có:
\(\dfrac{6}{\sqrt{x}-3}=3\\ \Leftrightarrow\dfrac{6}{\sqrt{x}-3}=\dfrac{3\sqrt{x}-9}{\sqrt{x}-3}\\ \Leftrightarrow6=3\sqrt{x}-9\\ \Leftrightarrow3\sqrt{x}=15\\ \Leftrightarrow\sqrt{x}=5\\ \Leftrightarrow x=25\)
vậy để B=3 thì x=25
30 tháng 6 2021
Bài 3:
a) Ta có: \(A=\left(\dfrac{\sqrt{x}}{\sqrt{x}+3}+\dfrac{3}{\sqrt{x}-3}\right)\cdot\dfrac{\sqrt{x}+3}{x+9}\)
\(=\dfrac{x-3\sqrt{x}+3\sqrt{x}+9}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\cdot\dfrac{\sqrt{x}+3}{x+9}\)
\(=\dfrac{1}{\sqrt{x}-3}\)
b) Ta có: \(B=21\left(\sqrt{2+\sqrt{3}}+\sqrt{3-\sqrt{5}}\right)^2-6\left(\sqrt{2-\sqrt{3}}+\sqrt{3+\sqrt{5}}\right)^2-15\sqrt{15}\)
\(=21\left(5+\sqrt{3}-\sqrt{5}+2\sqrt{\left(2+\sqrt{3}\right)\left(3-\sqrt{5}\right)}\right)-6\left(5-\sqrt{3}+\sqrt{5}+2\sqrt{\left(2-\sqrt{3}\right)\left(3+\sqrt{5}\right)}\right)-15\sqrt{15}\)
\(=21\left(4+\sqrt{15}\right)-6\left(4+\sqrt{15}\right)-15\sqrt{15}\)
\(=84+21\sqrt{15}-24-6\sqrt{15}-15\sqrt{15}\)
=60
21 tháng 12 2021
b: Vì (d)//(d') nên a=2
Vậy: y=2x+b
Thay x=1 và y=-2 vào (d), ta được:
b+2=-2
hay b=-4
\(1+tan^2a=\frac{1}{cos^2a}\)
=> cos a =\(\frac{\sqrt{10}}{10}\)
\(cos^2a+sin^2a=1\)
=> sin a = \(\frac{3\sqrt{10}}{10}\)
\(A=1\)