K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
19 tháng 12 2023
a: \(VP=a^3+b^3+c^3-3bac\)
\(=\left(a+b\right)^3+c^3-3ab\left(a+b\right)-3abc\)
\(=\left(a+b+c\right)\left[\left(a+b\right)^2-c\left(a+b\right)+c^2\right]-3ab\left(a+b+c\right)\)
\(=\left(a+b+c\right)\left(a^2+2ab+b^2-ac-bc+c^2-3ab\right)\)
\(=\left(a+b+c\right)\left(a^2+b^2+c^2-ab-bc-ac\right)=VT\)
b: \(VT=\left(3a+2b-1\right)\left(a+5\right)-2b\left(a-2\right)\)
\(=3a^2+15a+2ab+10b-a-5-2ab+4b\)
\(=3a^2+14a+14b-5\)
\(VP=\left(3a+5\right)\left(a+3\right)+2\left(7b-10\right)\)
\(=3a^2+9a+5a+15+14b-20\)
\(=3a^2+14a+14b-5\)
=>VT=VP
c: \(VT=a\left(b-x\right)+x\left(a+b\right)\)
\(=ab-ax+ax+bx\)
\(=ab+bx=b\left(a+x\right)=VP\)
d: \(VT=a\left(b-c\right)-b\left(a+c\right)+c\left(a-b\right)\)
\(=ab-ac-ab-bc+ca-cb\)
\(=-2bc\)
=VP
AH
Akai Haruma
Giáo viên
2 tháng 1
Lời giải:
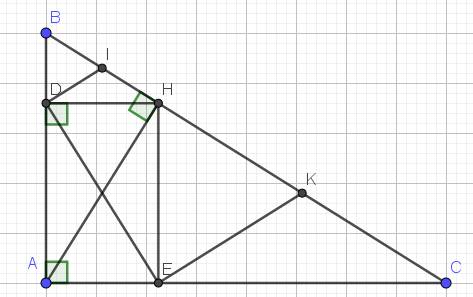
a. Xét tứ giác $ADHE$ có 3 góc vuông $\widehat{A}=\widehat{D}=\widehat{E}=90^0$ nên tứ giác $ADHE$ là hình chữ nhật.
b.
Xét tam giác vuông $BDH$ vuông tại $D$ có $DI$ là đường trung tuyến ứng với cạnh huyền $BH$ nên $DI=\frac{BH}{2}=IH$
$\Rightarrow DIH$ là tam giác vuông tại $I$
$\Rightarrow \widehat{IDH}=\widehat{IHD}$ (1)
$ADHE$ là hình chữ nhật nên $\widehat{HDE}=\widehat{HAE}=\widehat{HAC}$ (2)
Từ $(1); (2)\Rightarrow \widehat{IDH}+\widehat{HDE}=\widehat{IHD}+\widehat{HAC}$
$\Rightarrow \widehat{IDE}=\widehat{IHD}+\widehat{HAC}$.
Mà $\widehat{IHD}=\widehat{HCA}$ (2 góc đồng vị)
$\Rightarrow \widehat{IDE}=\widehat{HCA}+\widehat{HAC}=180^0-\widehat{AHC}=180^0-90^0=90^0$
$\Rightarrow DI\perp DE$
c. Tương tự phần a ta suy ra $DE\perp EK$
Vậy $DI\perp DE, EK\perp DE$
$\Rightarrow DI\parallel EK$ và $DI, EK$ cùng vuông góc với $DE$
$\Rightarrow DIKE$ là hình thang vuông.
d.
Có: $DI=\frac{BH}{2}\Rightarrow BH=2DI=2.1=2$ (cm)
$EK=\frac{CH}{2}\Rightarrow CH=2EK=8$ (cm)
$\Rightarrow BC=BH+CH=2+8=10$ (cm)
$S_{ABC}=AH.BC:2=6.10:2=30$ (cm2)
LC
1
21 tháng 11 2023
a: Xét ΔHAC vuông tại H và ΔABC vuông tại A có
\(\widehat{C}\) chung
Do đó: ΔHAC~ΔABC
b: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=15^2+20^2=625\)
=>BC=25
Xét ΔABC vuông tại A có AH là đường cao
nên \(\left\{{}\begin{matrix}BH\cdot BC=BA^2\\AH\cdot BC=AB\cdot AC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH\cdot25=15^2=225\\AH\cdot25=15\cdot20=300\end{matrix}\right.\)
=>BH=9; AH=12
1 tháng 7 2023
a: góc AEH=góc ADH=góc DAE=90 độ
=>AEHD là hcn
b: XétΔAEH vuông tại E và ΔAHC vuông tại H có
góc EAH chung
=>ΔAEH đồng dạng với ΔAHC
c: ΔAHC vuông tại H có HE là đường cao
nên HE^2=AE*EC
S
31 tháng 8 2021
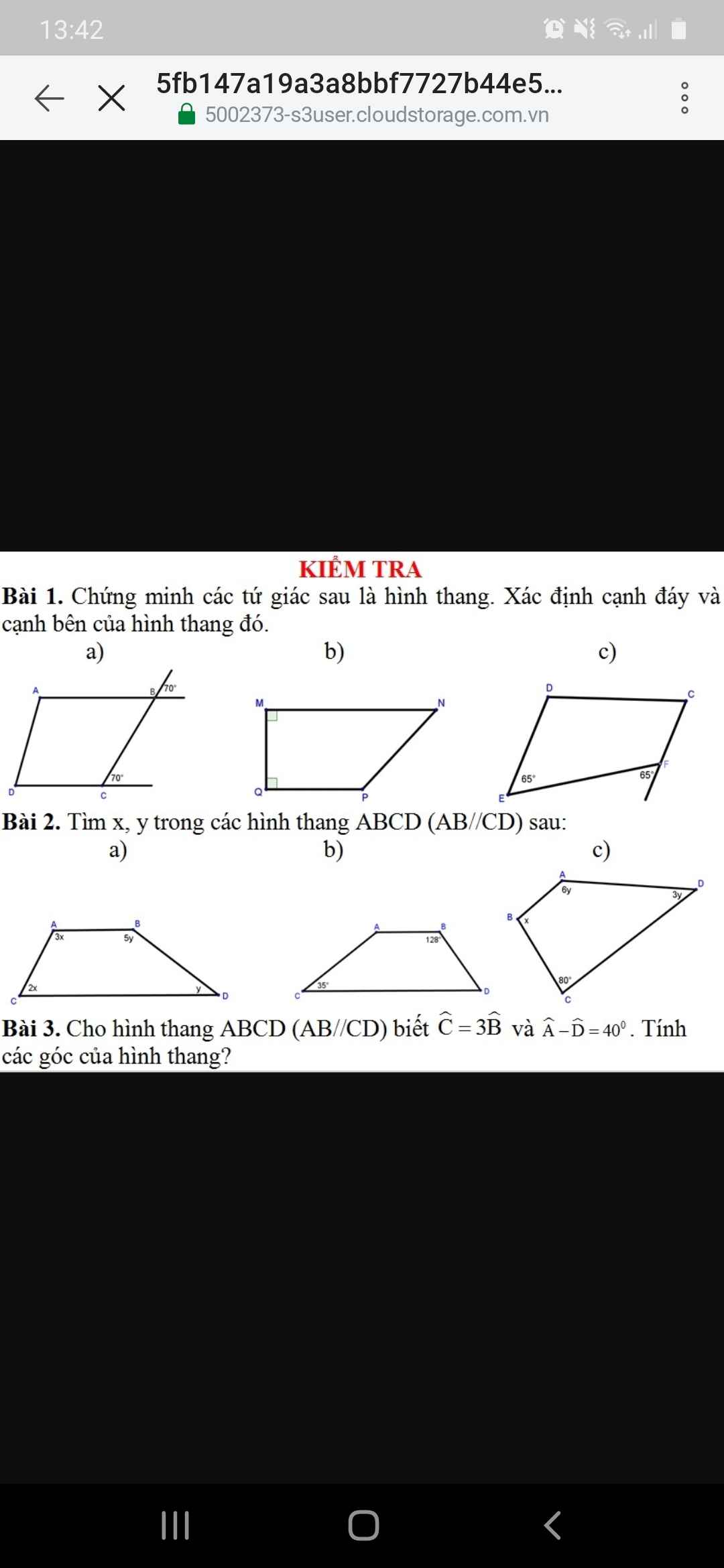
Bài 1
a) góc B=góc C=70 độ(gt)
=>AB//DC(đồng vị)
=> ABCD là hình thang
b)góc M+ góc Q=90 độ +90 độ=180 độ
=>MN//QP( hai góc trong cùng phía bù nhau)
=>MNPQ là hình thang
c)góc E= góc F=65 độ
=>DE//CF( slt)
=> DCFE là hình thang
20 tháng 12 2021
Bài 4:
b: Ta có: ΔAHC vuông tại H
mà HI là đường trung tuyến
nên IH=IC
hay ΔIHC cân tại I
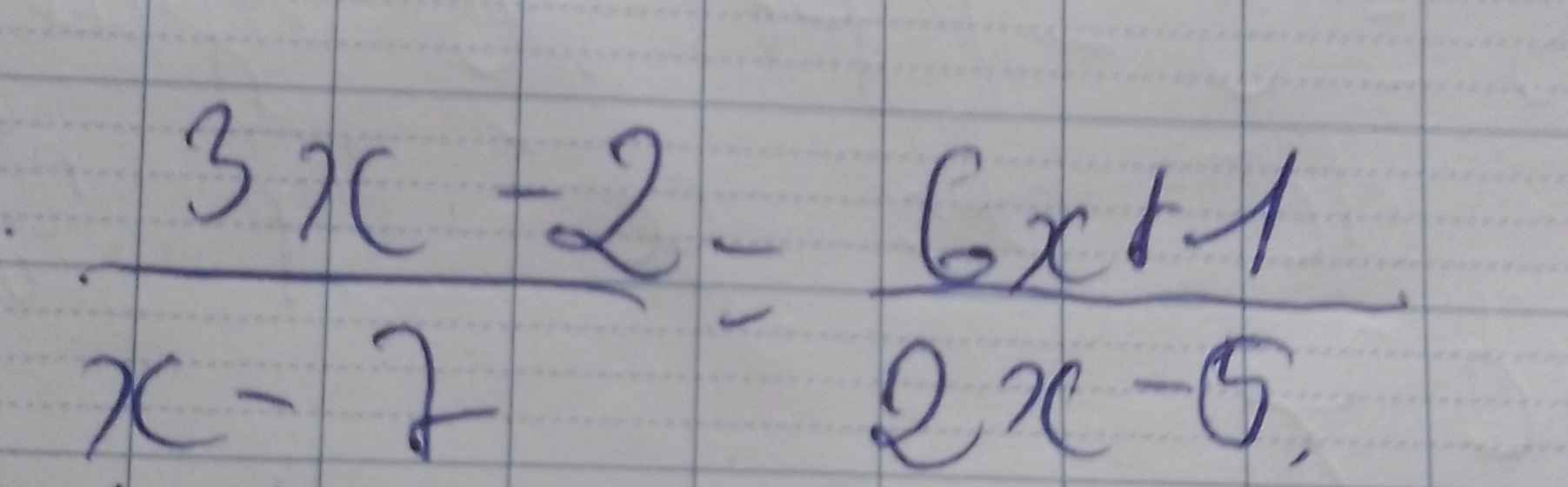
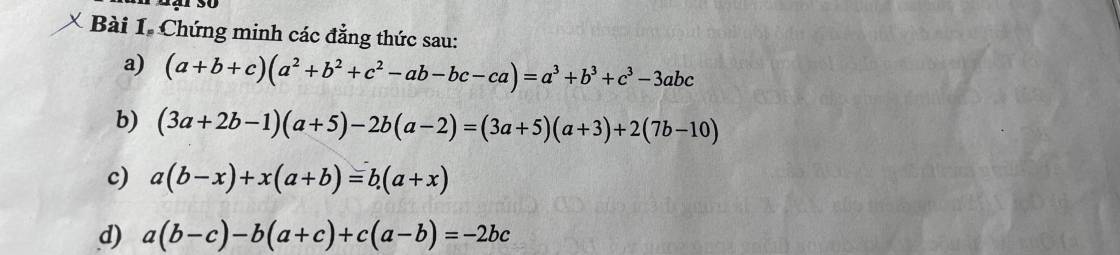
đkxđ : x khác 7 , x khác 5/2
\(\Leftrightarrow\dfrac{\left(3x-2\right)\left(2x-5\right)}{\left(x-7\right)\left(2x-5\right)}-\dfrac{\left(6x+1\right)\left(x-7\right)}{\left(2x-5\right)\left(x-7\right)}=0\)
<=> \(\dfrac{6x^2-15x-4x+10}{....}-\dfrac{6x^2-42x+x-7}{...}=0\)
<=> \(6x^2-19x+10-6x^2+41x+7=0\)
<=> 22x + 17 =0
<=> \(x=-\dfrac{17}{22}\) (tm)
Vậy..