Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

C1:A={0}
C2:Gọi A là tập họp các số tự nhiên ko vượt qua n.
A={0;1;2;3;...;n}
Số phần tử của tập A là:(n-0):1+1=n+1 phần tử
Có n+1 số tự nhiên.

Bài 3: Số đo góc
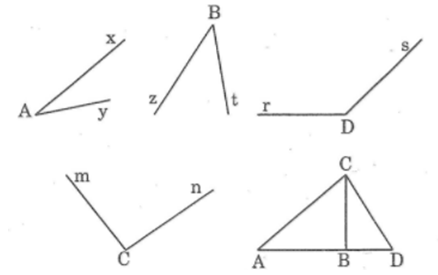
Bài 11 trang 84 sách bài tập Toán 6 Tập 2: 11. Xem hình dưới đây:
a) Ước lượng bằng mắt số đo mỗi góc rồi ghi vào bảng.
b) Dùng thước đo góc tìm số đo mỗi góc rồi ghi vào bảng.
c) Sắp xếp các góc theo thứ tự lớn dần.
Lời giải:
Dùng thước đo góc để đo và ghi vào bảng
a/ Đầu tiên cậu ước lượng số đo của các góc. Ví dụ: Góc xAy: 20 độ.
b/ Cậu dùng thước đo độ để đo góc chính xác của các góc. Ví dụ: Góc xAy: 25 độ.
c/ Cuối cùng cậu sắp xếp các góc với số đo chính xác của câu b theo thứ tự từ bé đến lớn.
k nha ^,^


a,Số bài tập hòa giải được trong buổi chiều là :
12x2/3=8(bài)
b,số bài tập giải được trong cả ngày hôm đó là :
12+8=20(bài)
tỉ số phần trăm của số bài tập giải được trong buổi chiều và số bài tập giải được trong cả ngày hôm đó là :
8:20x100=40%

Bài 1 :
a) A=37.36+20.37+44.37
A=37.(36+20+44)
A=37.100
A=3700
Bài 6 :
\(A=2^0+2^1+2^2+2^3+...+2^{2010}\)
\(2A=2+2^2+2^3+2^4+...+2^{2011}\)
\(2A-A=\left(2+2^2+2^3+2^4+...+2^{2011}\right)-\left(2^0+2^1+2^2+2^3+...+2^{2010}\right)\)
\(A=\left(2+2^2+2^3+2^4+...+2^{2010}\right)+2^{2011}-2^0-\left(2+2^2+2^3+2^4+...+2^{2010}\right)\)
\(A=2^{2011}-1\)
\(\Rightarrow A+1=2^{2011}\)
Vậy A đã có dạng lũy thừa cơ số là 2

Bài 11.5:
Ta có : A=3/4.8/9.15/16...899/900
=> A=(1.3/2.2).(2.4/3.3).(3.5/4.4)...(299.301/300.300)
=> A=((1.2.3...299).(3.4.5...301))/((2.3.4...300).(2.3.4...300))
=> A=1.301/2.300
=> A=301/600
Vậy A=301/600
Bài 11.6:
Ta có : 1/5=1/5;1/6<1/5:...:1/9<1/5:1/10<1/8;1/11<1/8;...1/17<1/8
=> (1/5+1/6+1/7+...+1/9)+(1/10+1/11+...+1/17)<(1/5+1/5+...+1/5)+(1/8+1/8+...+1/8) (có 5 số 1/5 và 8 số 1/8 )
=>A<1/5.5+1/8.8
=> A<2
Vậy bài toán được chứng minh.
Các bạn nhớ *** Cho mik nha !!!
bài 11.5
tích A = 1.3/2.2 x 2.4/3.3 x 3.5/4.4 ...29x 31 /30 x30 = 1x2x3 ...29/2x3x4 ... 30
= 1/30 x31/2
bai 11.6
1/5 + 1/6 + 1/7 + 1/8 + 1/9 < 1/5 x 5 = 1 (1)
1/10 + 1/11 +... + 1/16 + 1/17 < 1/8 x8 (2)
Từ 1 và 2 ta có 1/5 + 1/6 + ... + 1/17 < 2
k mình nhé bạn
mình là người làm cho bạn đầu tiên đó

Bài 37 trang 11 sách bài tập Toán 6 Tập 2: Bạn Minh đã tìm ra một cách "rút gọn" phân số rất đơn giản. Này nhé:
Em hãy kiểm tra xem các kết quả tìm được có đúng không?
Em có thể áp dụng "phương pháp" này để rút gọn các phân số có dạng ab/bc hay không?
Lời giải:
Kiểm tra ta thấy các kết quả tìm được đều đúng. Tuy nhiên, không thể áp dụng "phương pháp" trên để rút gọn các phân số có dạng ab/bc.
Ví dụ :
Cách "rút gọn" của bạn Minh chỉ đúng một cách ngẫu nhiên

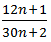 là phân số tối giản (n ∈ N)
là phân số tối giản (n ∈ N)
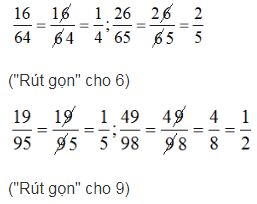
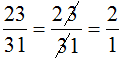
5 cách chọn ba trong bảy số để có tổng bằng 0 là:
5 cách chọn ba trong bảy số để có tổng bằng 0 là: