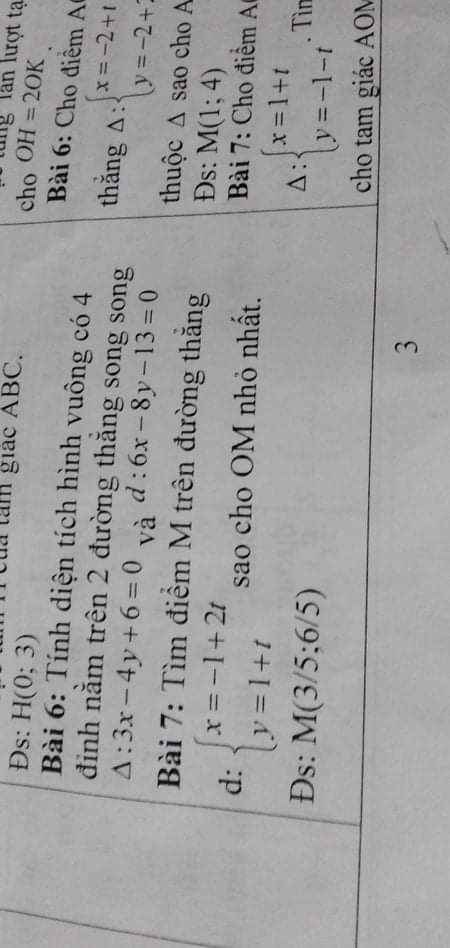NV
Giải dùm mình với mọi người ơi mình làm hong kiệp bài mn lm gấp dùm mình với
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
ND
1
DT
2
NT
1
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 4 2021
Do M thuộc d nên tọa độ có dạng: \(M\left(2t-1;t+1\right)\)
\(\Rightarrow\overrightarrow{OM}=\left(2t-1;t+1\right)\Rightarrow OM=\sqrt{\left(2t-1\right)^2+\left(t+1\right)^2}\)
\(OM=\sqrt{5t^2-2t+2}=\sqrt{5\left(t-\dfrac{1}{5}\right)^2+\dfrac{9}{5}}\ge\dfrac{3}{\sqrt{5}}\)
Dấu "=" xảy ra khi \(t-\dfrac{1}{5}=0\Rightarrow t=\dfrac{1}{5}\Rightarrow M\left(-\dfrac{3}{5};\dfrac{6}{5}\right)\)
Đáp án của bài toán bị sai (nhầm dấu hoành độ)
MN
31 tháng 3 2021
\(\left|1-2x\right|< 5-x\)
\(\Leftrightarrow-\left(5-x\right)< 1-2x< 5-x\)
\(\Leftrightarrow x-5< 1-2x< 5-x\)
\(\Leftrightarrow-4< x< 2\)
0P
0
KA
1
13 tháng 5 2021
`m=5`
`=>-20x+5-3=0`
`=>-20x+2=0`
`=>x=-1/10=>m=5` pt có nghiệm
Nếu `m ne 5=>` pt trên là pt bậc 2
ĐK để pt bậc 2 có nghiệm
`=>Delta'>0`
`<=>4m^2-(m-2)(m-5)>0`
`<=>4m^2-(m^2-7m+5)>0`
`<=>3m^2+7m-5>0`
`<=>m^2+7/3m-5/3>0`
`<=>(m+7/6)^2-109/36>0`
`<=>` \(\left[ \begin{array}{l}m>\dfrac{\sqrt{109}-7}{6}\\m<\dfrac{-\sqrt{109}-7}{6}\end{array} \right.\)