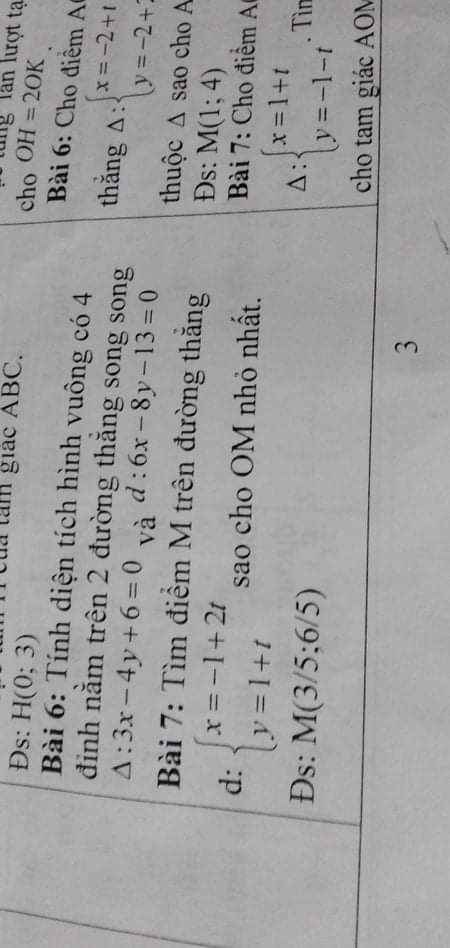Giải dùm đi mọi người
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HN
0
HI
0
AH
Akai Haruma
Giáo viên
24 tháng 9 2021
Lời giải:
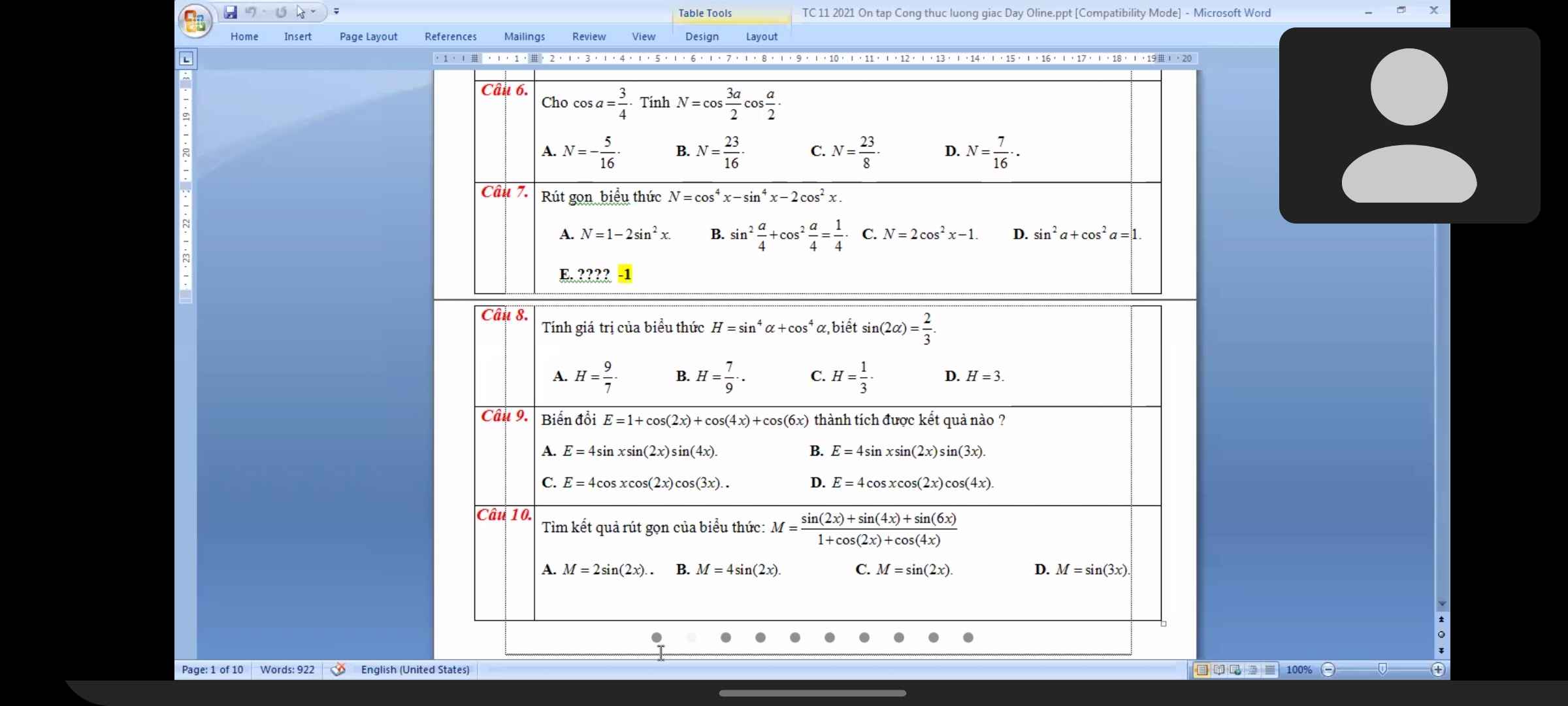
$H=(\sin ^2a+\cos ^2a)^2-2\sin ^2a\cos ^2a$
$=1-\frac{1}{2}(2\sin a\cos a)^2=1-\frac{1}{2}(\sin 2a)^2=1-\frac{2}{9}=\frac{7}{9}$
Đáp án B.
0D
3
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 3 2022
7.3
Đường thẳng \(\Delta_1\) có 1 vtcp là (2;5) nên nhận (5;-2) là 1 vtpt và đi qua điểm có tọa độ (1;3)
Do đó pt tổng quát của \(\Delta_1\) là:
\(5\left(x-1\right)-2\left(y-3\right)=0\Leftrightarrow5x-2y+1=0\)
b. Đường thẳng \(\Delta_2\) có 1 vtpt là (2;3) nên có 1 vtcp là \(\left(3;-2\right)\)
Chọn \(A\left(1;1\right)\) là 1 điểm thuộc \(\Delta_2\)
Phương trình tham số \(\Delta_2\): \(\left\{{}\begin{matrix}x=1+3t\\y=1-2t\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 4 2021
Do M thuộc d nên tọa độ có dạng: \(M\left(2t-1;t+1\right)\)
\(\Rightarrow\overrightarrow{OM}=\left(2t-1;t+1\right)\Rightarrow OM=\sqrt{\left(2t-1\right)^2+\left(t+1\right)^2}\)
\(OM=\sqrt{5t^2-2t+2}=\sqrt{5\left(t-\dfrac{1}{5}\right)^2+\dfrac{9}{5}}\ge\dfrac{3}{\sqrt{5}}\)
Dấu "=" xảy ra khi \(t-\dfrac{1}{5}=0\Rightarrow t=\dfrac{1}{5}\Rightarrow M\left(-\dfrac{3}{5};\dfrac{6}{5}\right)\)
Đáp án của bài toán bị sai (nhầm dấu hoành độ)