K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NY
28 tháng 4 2015
* Điều kiện để 2 đồ thị hàm số vuông góc với nhau.a.a'=-1
* Điều kiện để 2 đồ thị hàm số cắt nhau tại 1 điểm trên trục hoành.a khác a'
và b/a khác b'/a'
* Điều kiện để 2 đồ thị hàm số cắt nhau tại một điểm trên trục tung a khác a'
và b=b'
* Điều kiện để 2 đồ thị hàm số song song với nhau a=a'
và b khác b'
* Điều kiện để 2 đồ thị hàm số cắt nhau.a khác a'
* Điều kiện để 2 đồ thị hàm số trùng nhau.a=a' và b=b'
* Điều kiện để 2 đồ thị hàm số song song và cắt nhau trên trục tung kết hợp lần lượt of 2 điều kiện
5 tháng 12 2021
a, Thay x = -2 => y = -2 + 4 = 2 => A(-2;2)
(d) cắt y = x + 4 tại A(-2;2) <=> 2 = -2 ( m + 1 ) - 2
<=> -2m - 2 - 2 = 2 <=> -2m = 6 <=> m = -3
Vậy (d) : y = -2x - 2
b, bạn tự vẽ nhé
c, Cho x = 0 => y = -2
=> (d) cắt trục Oy tại A(0;-2) => OA = | -2 | = 2
Cho y = 0 => x = -1
=> (d) cắt trục Ox tại B(-1;0) => OB = | -1 | = 1
Ta có : \(S_{OAB}=\frac{1}{2}.OA.OB=\frac{1}{2}.2.1=1\)( dvdt )
5 tháng 12 2021
Đặt: (d): y = (m+5)x + 2m - 10
Để y là hàm số bậc nhất thì: m + 5 # 0 <=> m # -5
Để y là hàm số đồng biến thì: m + 5 > 0 <=> m > -5
(d) đi qua A(2,3) nên ta có:
3 = (m+5).2 + 2m - 10
<=> 2m + 10 + 2m - 10 = 3
<=> 4m = 3
<=> m = 3/4
(d) cắt trục tung tại điểm có tung độ bằng 9 nên ta có:
9 = (m+5).0 + 2m - 10
<=> 2m - 10 = 9
<=> 2m = 19
<=> m = 19/2
(d) đi qua điểm 10 trên trục hoành nên ta có:
0 = (m+5).10 + 2m - 10
<=> 10m + 50 + 2m - 10 = 0
<=> 12m = -40
<=> m = -10/3
(d) // y = 2x - 1 nên ta có:
\hept{m+5=22m−10≠−1\hept{m+5=22m−10≠−1 <=> \hept{m=−3m≠92\hept{m=−3m≠92 <=> m=−3
Giả sử (d) luôn đi qua điểm cố định M(x0; y0)
Ta có: y0=(m+5)x0+2m−10y0=(m+5)x0+2m−10
<=> mx0+5x0+2m−10−y0=0mx0+5x0+2m−10−y0=0
<=> m(xo+2)+5x0−y0−10=0m(xo+2)+5x0−y0−10=0
Để M cố định thì: \hept{x0+2=05x0−y0−10=0\hept{x0+2=05x0−y0−10=0 <=> \hept{x0=−2y0=−20\hept{x0=−2y0=−20
Vậy...
KV
20 tháng 5 2023
1) Hàm số đồng biến khi x > 0 và nghịch biến khi x < 0
Bảng giá trị:
Đồ thị:
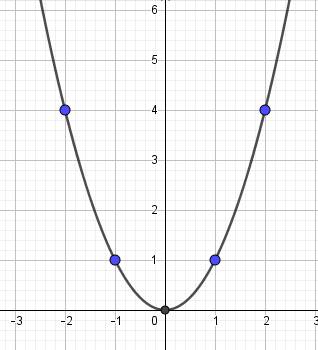
2) Thay tọa độ điểm M(3; 9) vào (P) ta được:
\(9=3^2\) (đúng)
Vậy điểm M(3; 9) thuộc đồ thị (P)
AS
a, Cách vẽ đồ thị hàm số y=x^2 và y=2x-1
b, bằng cách giải PT xác định tọa độ giao điểm 2 đồ thị trên
1
5 tháng 5 2015
a) Đồ thị hàm số y = x2 là parabol đi qua 3 điểm O(0; 0); A(1;1); B(-1; 1) ; nhận trục Oy là trục đối xứng
+) Đồ thị hàm số y = 2x -1 là đường thẳng đi qua 2 điểm C(0; -1); D(1/2; 0)
b) Hoành độ giao điểm là nghiệm của phương trình: x2 = 2x - 1 => x2 - 2x + 1 = 0 => (x -1)2 = 0 => x = 1
=> y = 1
Vậy toạ độ giao điểm của hai đồ thị hàm số là điểm (1;1)