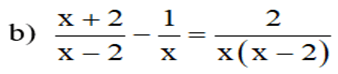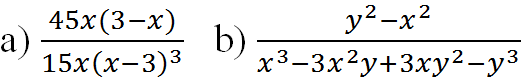K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
KV
13 tháng 11 2018
Đề bài
Cho hình thang ABCD (AB, CD là hai đáy). Gọi M, N, P, Q lần lượt là trung điểmcủa AB, AC, CD, BD.
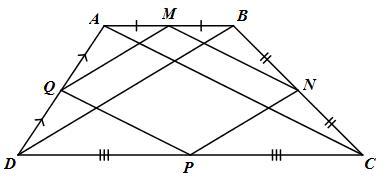
a) M, N lần lượt là trung điểm của AB và BC (gt);
⇒MN⇒MN là đường trung bình của tam giác ABC
⇒MN//AC⇒MN//AC và ..
Q, P lần lượt là trung điểm của AD và CD (gt);
⇒QP⇒QP là đường trung bình của tam giác ADC
⇒QP//AC⇒QP//AC và QP=12AC(2)QP=12AC(2)
Từ (1) và (2) ⇒MN//QP⇒MN//QP và MN=QPMN=QP
Vậy tư giác MNPQ là hình bình hành.
b) Ta có tứ giác MNPQ là hình bình hành.
MN // AC, MN=AC2MN=AC2 (MN là đường trung bình của tam giác ABC)
MQ // BD, MQ=BD2MQ=BD2 (MQ là đường trung bình của tam giác ABD)
* Tứ giác MNPQ là hình thoi ⇔⇔ Hình bình hành MNPQ có MN=MQ⇔AC=BDMN=MQ⇔AC=BD
Vậy hình thanh ABCD cần có thêm điều kiện AC=BDAC=BD để tứ giác MNPQ là hình thoi.
* Tứ giác MNPQ là hình chữ nhật ⇔⇔ Hình bình hành MNPQ có ˆNMQ=900NMQ^=900
⇒MN⊥MQ⇔MQ⊥AC⇔AC⊥BD⇒MN⊥MQ⇔MQ⊥AC⇔AC⊥BD
Vậy hình thang ABCD cần có thêm điều kiện AC⊥BDAC⊥BD để tứ giác MNPQ là hình chữ nhật.
* Tứ giác MNPQ là hình vuông ⇔⇔ Hình thoi MNPQ có ˆNMQ=900⇔AC=BDNMQ^=900⇔AC=BD và AC⊥BDAC⊥BD
Vậy hình thang ABCD cần thêm điều kiện AC=BD,AC⊥BDAC=BD,AC⊥BD để tứ giác MNPQ là hình vuông.
Xem thêm tại: https://loigiaihay.com/bai-tap-2-trang-140-tai-lieu-day-hoc-toan-8-tap-1-c242a43131.html#ixzz5Y0XJF4SV
21 tháng 5 2019
a) |3x| = x + 6 (1)
Ta có 3x = 3x khi x ≥ 0 và 3x = -3x khi x < 0
Vậy để giải phương trình (1) ta quy về giải hai phương trình sau:
+ ) Phương trình 3x = x + 6 với điều kiện x ≥ 0
Ta có: 3x = x + 6 ⇔ 2x = 6 ⇔ x = 3 (TMĐK)
Do đó x = 3 là nghiệm của phương trình (1).
+ ) Phương trình -3x = x + 6 với điều kiện x < 0
Ta có -3x = x + 6 ⇔ -4x + 6 ⇔ x = -3/2 (TMĐK)
Do đó x = -3/2 là nghiệm của phương trình (1).
Vậy tập nghiệm của phương trình đã cho S = {3; -3/2}
c) (x + 1)(2x – 2) – 3 > –5x – (2x + 1)(3 – x)
⇔ 2x2 – 2x + 2x – 2 – 3 > –5x – (6x – 2x2 + 3 – x)
⇔ 2x2 – 5 ≥ –5x – 6x + 2x2 – 3 + x
⇔ 10x ≥ 2 ⇔ x ≥ 1/5
Tập nghiệm: S = {x | x ≥ 1/5}
21 tháng 5 2019
a) |3x|=x+6
Với |3x|=3x ta có:
<=>3x=x+6
<=> 3x-x=6
<=> 2x=6
<=>x=3
Vậy pt có nghiệm x=3
NV
1
17 tháng 3 2023
đây bạn nha đề này mik cũng đang giải mà chưa hết:
11 tháng 4 2019
https://nguyentuc2thanhmy.violet.vn/present/de-thi-hsg-toan-8-thanh-chuong-2010-2015-11572578.html
https://thcs-nghiaan-nghean.violet.vn/present/hsg-toan-8-nghia-dan-15-16-12511169.html
4 tháng 2 2021
Câu 1:
a) Ta có: 7x+21=0
\(\Leftrightarrow7x=-21\)
hay x=-3
Vậy: S={-3}
b) Ta có: 3x-2=2x-3
\(\Leftrightarrow3x-2-2x+3=0\)
\(\Leftrightarrow x+1=0\)
hay x=-1
Vậy: S={-1}
c) Ta có: 5x-2x-24=0
\(\Leftrightarrow3x=24\)
hay x=8
Vậy: S={8}
Câu 2:
a) Ta có: \(\left(2x+1\right)\left(x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2x+1=0\\x-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=-1\\x=1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{2}\\x=1\end{matrix}\right.\)
Vậy: \(S=\left\{-\dfrac{1}{2};1\right\}\)
b) Ta có: \(\left(2x-3\right)\left(-x+7\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-3=0\\-x+7=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=3\\-x=-7\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=7\end{matrix}\right.\)
Vậy: \(S=\left\{\dfrac{3}{2};7\right\}\)
c) Ta có: \(\left(x+3\right)^3-9\left(x+3\right)=0\)
\(\Leftrightarrow\left(x+3\right)\left[\left(x+3\right)^2-9\right]=0\)
\(\Leftrightarrow\left(x+3\right)\left(x+3-3\right)\left(x+3+3\right)=0\)
\(\Leftrightarrow x\left(x+3\right)\left(x+6\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x+3=0\\x+6=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-3\\x=-6\end{matrix}\right.\)
Vậy: S={0;-3;-6}
18 tháng 1 2019
\(\sqrt[3]{2x+2}=x^3+9x^2+26x+28\)
\(\Rightarrow\left(2x+2\right)^3=\left(x+3\right)^3+1\)
\(\Rightarrow\left(2x+2\right)^3-\left(x+3\right)^3=1\)
\(\Rightarrow\left(2x+2-x-3\right)\left[\left(2x+2\right)^2+\left(2x+2\right)+\left(x+3\right)^2\right]=1\cdot1=\left(-1\right)\left(-1\right)\)
\(\Rightarrow\left(x-1\right)\left[\left(2x+2\right)^2+\left(2x+2\right)\left(x+3\right)+\left(x+3\right)^2\right]=1\cdot1=\left(-1\right)\left(-1\right)\)
Với:\(x-1=1\Rightarrow x=2\)
Thay vào thừa số thứ 2 thấy sai nên loại
Với:\(x-1=-1\)
\(\Rightarrow x=0\)
Thay vào thừa số thứ 2 thấy sai nên loại.
Vậy phương trình vô nghiệm.
tth xem có đúng ko nha!cao cấp quá!Nếu sai thì ib vs mình:))
