Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đăng mấy câu lớp 9 thì bó tay !
- tôi ko có bít
- ???????
- tự làm nhé
- k tui nha !
- kb vs tui nha !
- chuk bn may mắn


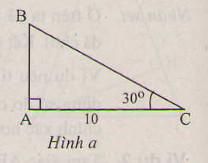
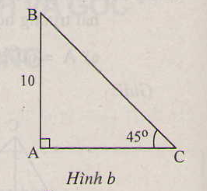
a: \(\widehat{B}=45^0\)
\(b=c=10cm\)
\(a=\sqrt{2\cdot b^2}=10\sqrt{2}\left(cm\right)\)
b: \(\widehat{C}=90^0-35^0=55^0\)
\(b=a\cdot\sin B=11,47\left(cm\right)\)
\(c=\sqrt{a^2-b^2}=16,38\left(cm\right)\)

a: \(\widehat{C}=90^0-58^0=32^0\)
Xet ΔABC vuông tại A có \(\sin B=\dfrac{AC}{BC}\)
nên \(AC=BC\cdot\sin B=72\cdot\sin58^0\simeq61,06\left(cm\right)\)
\(AB=\sqrt{BC^2-AB^2}=\sqrt{72^2-61.06^2}=38.15\left(cm\right)\)
b: \(\widehat{C}=90^0-48^0=42^0\)
Xét ΔABC vuông tại A có
\(AC=BC\cdot\cos C\)
nên \(BC=\dfrac{20}{\cos42^0}\simeq26.91\left(cm\right)\)
\(AB=\sqrt{26.91^2-20^2}=18.004\left(cm\right)\)
c: \(\widehat{B}=90^0-30^0=60^0\)
Xét ΔABC vuông tại A có
\(b=AC=BC\cdot\sin B\)
nên \(BC=\dfrac{AC}{\sin60^0}=\dfrac{15}{\sin60^0}=10\sqrt{3}\left(cm\right)\)
=>\(AB=\sqrt{\left(10\sqrt{3}\right)^2-15^2}=5\sqrt{3}\left(cm\right)\)

\(VT=a\left(\frac{1}{b}+\frac{1}{c}\right)+b\left(\frac{1}{c}+\frac{1}{a}\right)+c\left(\frac{1}{a}+\frac{1}{b}\right)\)
\(\ge a.\frac{4}{b+c}+b.\frac{4}{c+a}+c.\frac{4}{a+b}=4\left(\frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b}\right)\)

A B C H
a ) Ta có : \(20^2=12^2+16^2\Leftrightarrow BC^2=AB^2+AC^2\)
Theo định lý Pytago đảo thì tam giác ABC là tam giác vuông
b )
Áp dụng hệ thức lượng vào tam giác vuông ABC ta có :
\(AB.AC=AH.BC\Leftrightarrow AH=\frac{AB.AC}{BC}=\frac{12.16}{20}=9,6\left(cm\right)\)
c ) Ta có :
\(AB.cosB+AC.cosC=\frac{AB.AB}{BC}+\frac{AC.AC}{BC}\)
\(=\frac{AC^2+AB^2}{BC}=\frac{BC^2}{BC}=BC=20\left(cm\right)\)
Chúc bạn học tốt !!!

1. Hình:
A B C H M
~~~
a/Ta có: \(\widehat{C}=90^o-\widehat{B}=90^o-30^o=60^o\)
Theo tỉ số lượng giác có:
\(sin\widehat{B}=\dfrac{AC}{BC}\)\(\Rightarrow BC=\dfrac{AC}{sin\widehat{B}}=\dfrac{6}{sin30^o}=12\left(cm\right)\)
Áp dụng pitago vào tam giác ABC v tại A có: BC2 = AB2 + AC2
hay 122 = AB2 + 62
=> AB2 = 122 - 62 = 108
=> AB = \(6\sqrt{3}\approx10,4\left(cm\right)\)
b/ Có: AH _|_ BC
Theo hệ thức lượng có:
AB2 = BC . BH
=> \(BH=\dfrac{AB^2}{BC}=\dfrac{10,4^2}{12}\approx9\left(cm\right)\)
AM là trung truyến của t/g ABC => AM = 1/2BC = 6(cm)
=> HM = BH - BM = 9 - 6 = 3(cm)
xét tam giác AHM có góc H = 90o, theo pitago có:
\(AM^2=AH^2+HM^2\Rightarrow AH^2=AM^2-HM^2=6^2-3^2=27\Rightarrow AH\approx5,2\left(cm\right)\)
=> \(S_{\Delta AHM}=\dfrac{1}{2}\cdot HM\cdot AH=\dfrac{1}{2}\cdot3\cdot5,2=7,8\left(cm^2\right)\)
nốt bài 2.........
A B C D H
~~~
a, theo tỉ số lg giác có:
\(sinC=\dfrac{AB}{BC}\Rightarrow BC=\dfrac{AB}{sinC}=\dfrac{10}{sin40^o}\approx15,6\left(cm\right)\)
b, A/dung pitago vào t/g ABC v tại A
=> \(AC=\sqrt{BC^2-AB^2}=\sqrt{15,6^2-10^2}\approx12\left(cm\right)\)
vì AD là p/g góc A nên:
\(\dfrac{BD}{AB}=\dfrac{CD}{AC}=\dfrac{AD+CD}{AB+AC}=\dfrac{BC}{10+12}=\dfrac{15,6}{22}=\dfrac{39}{55}\Rightarrow BD=\dfrac{39}{55}\cdot AB=\dfrac{39}{55}\cdot10\approx7,1\left(cm\right)\)
kẻ AH _|_ BC:
a/d hệ thức lượng có:
\(\left\{{}\begin{matrix}AB^2=BC\cdot BH\\BC\cdot AH=AB\cdot AC\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}BH=\dfrac{AB^2}{BC}=\dfrac{10^2}{15,6}\approx6,4\left(cm\right)\\AH=\dfrac{AB\cdot AC}{BC}=\dfrac{10\cdot12}{15,6}\approx7,69\left(cm\right)\end{matrix}\right.\)
Ta có: HD = BD - BH = 7,1 - 6,4 = 0,7(cm)
A/dung pitago vào tam giác AHD v tại H có:
\(AD^2=AH^2+HD^2=7,69^2+0,7^2=59,78\Rightarrow AD\approx7,72\left(cm\right)\)