
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi số vở 7A,7B,7C ll là a,b,c(quyển;a,b,c∈N*)
Áp dụng tc dstbn:
\(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{4}=\dfrac{a+c}{2+4}=\dfrac{120}{8}=15\\ \Rightarrow\left\{{}\begin{matrix}a=30\\b=45\\c=60\end{matrix}\right.\)
Vậy ...

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{3}=\dfrac{y}{2}=\dfrac{x+y}{3+2}=\dfrac{15}{5}=3\)
Do đó: x=9; y=6

1. \(\left(2x^2-3x+1\right)+\left(3x^2+2x-1\right)\)
\(=2x^2-3x+1+3x^2+2x-1\)
\(=\left(2x^2+3x^2\right)-\left(3x-2x\right)+\left(1-1\right)\)
\(=5x^2-x\)
2. \(\left(4x^3-2x^2+3x\right)-\left(2x^3+3x^2-4x\right)\)
\(=4x^3-2x^2+3x-2x^3-3x^2+4x\)
\(=\left(4x^3-2x^3\right)-\left(2x^2+3x^2\right)+\left(3x+4x\right)\)
\(=2x^3-5x^2+7x\)
3. \(\left(x^2-5x+6\right)+\left(-3x^2+2x-1\right)\)
\(=x^2-5x+6-3x^2+2x-1\)
\(=\left(x^2-3x^2\right)-\left(5x-2x\right)+\left(6-1\right)\)
\(=-2x^2-3x+5\)
4. \(\left(2x^3+5x^2-3x+1\right)-\left(x^3-2x^2+x-1\right)\)
\(=2x^3+5x^2-3x+1-x^3+2x^2-x+1\)
\(=\left(2x^3-x^3\right)+\left(5x^2+2x^2\right)-\left(3x+x\right)+\left(1+1\right)\)
\(=x^3+7x^2-4x+2\)
5. \(\left(3x^2+2x-4\right)+\left(4x^2-x+5\right)\)
\(=3x^2+2x-4+4x^2-x+5\)
\(=\left(3x^2+4x^2\right)+\left(2x-x\right)-\left(4-5\right)\)
\(=7x^2+x+1\)
6. \(\left(x^3-2x^2+5x-1\right)-\left(2x^3+3x^2-4x+2\right)\)
\(=x^3-2x^2+5x-1-2x^3-3x^2+4x-2\)
\(=\left(x^3-2x^3\right)-\left(2x^2+3x^2\right)+\left(5x+4x\right)-\left(1+2\right)\)
\(=-x^3-5x^2+9x-3\)

Câu 15:
a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó: ΔBAD=ΔBED
Suy ra: DA=DE
b: Xét ΔADF vuông tại A và ΔEDC vuông tại E có
DA=DE
\(\widehat{ADF}=\widehat{EDC}\)
DO đó: ΔADF=ΔEDC
Suy ra: DF=DC
c: Ta có: ΔBFC cân tại B
mà BD là phân giác
nên BD là đường cao

a: Xét ΔABK và ΔACK có
AB=AC
\(\widehat{BAK}=\widehat{CAK}\)
AK chung
Do đó: ΔABK=ΔACK

a, Theo định lí Pytago tam giác ABH vuông tại H
\(AH=\sqrt{AB^2-BH}=\sqrt{81-9}=6\sqrt{2}\)
Theo định lí Pytago tam giác AHC vuông tại H
\(HC=x=\sqrt{AC^2-AH^2}=7\)
b, Xét tam giác ABC vuông tại A, đường cao AH
* Áp dụng hệ thức : \(AC^2=HC.BC=1600\Rightarrow AC=x=40\)

`a,`
`P(x)=x^2-5+x^4-4x^3-x^6`
`P(x)= -x^6+x^4-4x^3+x^2-5`
`Q(x)=2x^5-x^4+x^2-x^3+x-1`
`Q(x)=2x^5-x^4-x^3+x^2+x-1`
`b,`
`P(x)+Q(x)=(-x^6+x^4-4x^3+x^2-5)+(2x^5-x^4-x^3+x^2+x-1)`
`= -x^6+x^4-4x^3+x^2-5+2x^5-x^4-x^3+x^2+x-1`
`= -x^6+2x^5+(x^4-x^4)+(-4x^3-x^3)+(x^2+x^2)+x+(-5-1)`
`= -x^6+2x^5-5x^3+2x^2+x-6`
`c,`
`P(x)-Q(x)=(-x^6+x^4-4x^3+x^2-5)-(2x^5-x^4-x^3+x^2+x-1)`
`= -x^6+x^4-4x^3+x^2-5-2x^5+x^4+x^3-x^2-x+1`
`= -x^6-2x^5+(x^4+x^4)+(-4x^3+x^3)+(x^2-x^2)+x+(-5+1)`
`= -x^6-2x^5+2x^4-3x^3+x-4`
Ote.
Phần trừ đa thức một biến, bạn phải chú ý trước có dấu trừ, bạn ngoặc vào nhé! Còn trước dấu ngoặc có dấu trừ, đổi dấu. Khi gộp và rút gọn các đa thức cùng bậc, chú ý trước dấu ngoặc nên để dấu cộng, khi gộp vào phải đưa nguyên dấu của hạng tử, không được tự tiện đổi. Những cái này là phải nhớ nhé!
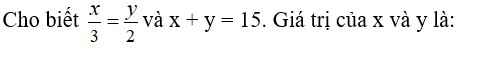
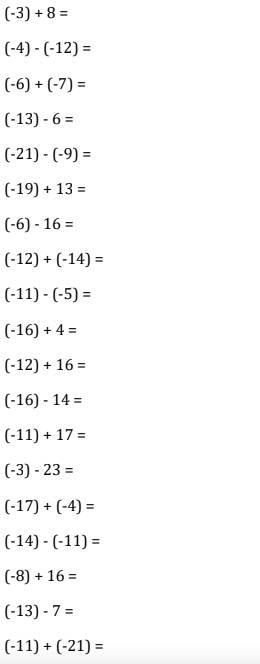
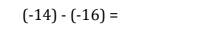





 chỉ mình cách giải với ! cảm ơn mấy bạn trước nha !
chỉ mình cách giải với ! cảm ơn mấy bạn trước nha !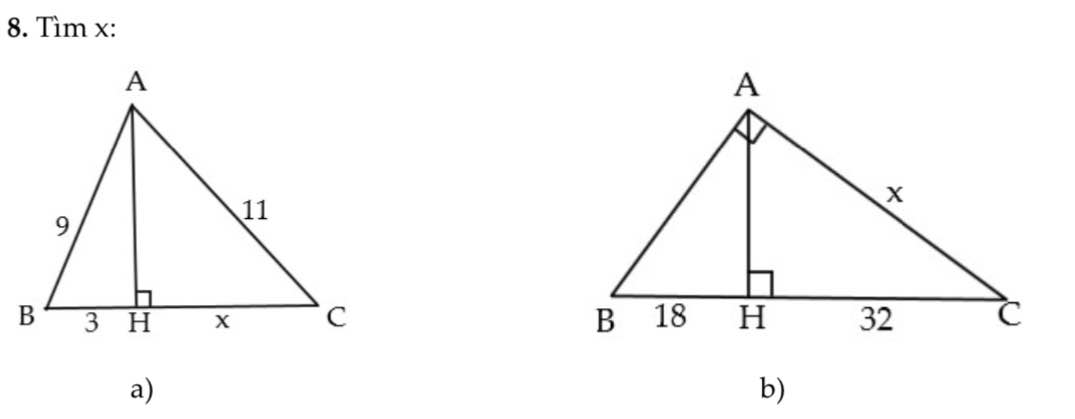
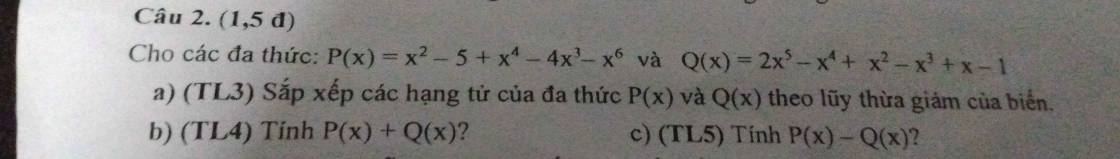 giải giúp mình nhé, cảm ơn mọi người và vote 5 điểm nha
giải giúp mình nhé, cảm ơn mọi người và vote 5 điểm nha
a.\(-\sqrt{x+1}\le0\)
Dấu "=" xảy ra \(\Leftrightarrow x=-1\)
\(\Rightarrow A=-\sqrt{x+1}+5\le5\)
Dấu "=" xảy ra \(\Leftrightarrow x=-1\)
Vậy \(A_{max}=5\Leftrightarrow x=-1\)
b.\(-\sqrt{x-1}\ge0\)
Dấu "=" xảy ra \(\Leftrightarrow x=1\)
\(\Rightarrow A=\sqrt{x+1}+5\ge2\)
Dấu "=" xảy ra \(\Leftrightarrow x=1\)
Vậy \(B_{min}=2\Leftrightarrow x=1\)
a) ĐK: \(x\ge-1\)
Có \(-\sqrt{x+1}\le0\forall x\ge-1\)
\(\Rightarrow A\le5\) \(\Rightarrow max_A=5\)
dấu "=" xảy ra \(\Leftrightarrow-\sqrt{x+1}=0\Leftrightarrow x=-1\)
b) ĐK: \(x\ge1\)
Ta có \(\sqrt{x-1}\ge0\forall x\ge1\)
\(\Rightarrow B\ge2\Rightarrow min_B=2\)
dấu "=" xảy ra <=> x=1