
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a:
ĐKXĐ: \(\left\{{}\begin{matrix}a>0\\a< >1\end{matrix}\right.\)
\(P=\left(\dfrac{\sqrt{a}+1}{\sqrt{a}-1}-\dfrac{\sqrt{a}-1}{\sqrt{a}+1}+4\sqrt{a}\right)\cdot\left(\sqrt{a}-\dfrac{1}{\sqrt{a}}\right)\)
\(=\dfrac{\left(\sqrt{a}+1\right)^2-\left(\sqrt{a}-1\right)^2+4\sqrt{a}\left(a-1\right)}{a-1}\cdot\dfrac{a-1}{\sqrt{a}}\)
\(=\dfrac{a+2\sqrt{a}+1-a+2\sqrt{a}-1+4\sqrt{a}\left(a-1\right)}{\sqrt{a}}\)
\(=\dfrac{4\sqrt{a}+4\sqrt{a}\left(a-1\right)}{\sqrt{a}}\)
=4+4(a-1)
=4a
b: \(a=\left(2+\sqrt{3}\right)\left(\sqrt{3}-1\right)\sqrt{2-\sqrt{3}}\)
\(=\left(2\sqrt{3}-2+3-\sqrt{3}\right)\cdot\dfrac{\sqrt{4-2\sqrt{3}}}{\sqrt{2}}\)
\(=\left(\sqrt{3}+1\right)\cdot\dfrac{\left(\sqrt{3}-1\right)}{\sqrt{2}}=\dfrac{3-1}{\sqrt{2}}=\sqrt{2}\)
Khi \(a=\sqrt{2}\) thì \(P=4\cdot\sqrt{2}=4\sqrt{2}\)

Bài 2:
b: Ta có: \(B=\dfrac{15-5\sqrt{x}}{x-5\sqrt{x}+6}+\dfrac{\sqrt{x}+3}{\sqrt{x}-2}\)
\(=\dfrac{-5\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}+\dfrac{\sqrt{x}+3}{\sqrt{x}-2}\)
\(=\dfrac{\sqrt{x}-2}{\sqrt{x}-2}=1\)

Do (d) đi qua C và D, thay tọa độ C và D vào pt (d) ta được:
\(\left\{{}\begin{matrix}a.\left(-1\right)+b=1\\a.\left(-2\right)+b=-3\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}-a+b=1\\-2a+b=-3\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}a=4\\b=5\end{matrix}\right.\)
Phương trình (d) có dạng: \(y=4x+5\)

tan B=3/4
=>AC/AB=3/4
=>AC=4,5
BC=căn AB^2+AC^2=7,5
sin C=AB/BC=6/7,5=4/5
cos C=AC/BC=3/5
tan C=4/3
cot C=3/4

Ta có
\(a^2+1=a^2+ab+bc+ca=a\left(a+b\right)+c\left(a+b\right)=\left(a+b\right).\left(a+c\right)\\ Cmtt:b^2+1=\left(b+a\right).\left(b+c\right)\\ c^2+1=\left(c+a\right).\left(c+b\right)\)
Nên
\(\dfrac{b-c}{a^2+1}+\dfrac{c-a}{b^2+1}+\dfrac{a-b}{c^2+1}\\ =\dfrac{\left(b-c\right)}{\left(a+b\right)\left(a+c\right)}+\dfrac{\left(c-a\right)}{\left(b+c\right)\left(b+a\right)}+\dfrac{\left(a-b\right)}{\left(c+a\right)\left(c+b\right)}\\ =\dfrac{\left(b-c\right)\left(b+c\right)+\left(c-a\right)\left(c+a\right)+\left(a-b\right)\left(a+b\right)}{\left(a+b\right)\left(b+c\right)\left(c+a\right)}\\ =\dfrac{b^2-c^2+c^2-a^2+a^2-b^2}{\left(a+b\right)\left(b+c\right)\left(c+a\right)}\\ =0\)
\(\dfrac{b-c}{a^2+1}+\dfrac{c-a}{b^2+1}+\dfrac{a-b}{c^2+1}\)
\(=\dfrac{b-c}{a^2+ab+bc+ac}+\dfrac{c-a}{b^2+ab+bc+ca}+\dfrac{a-b}{c^2+ab+bc+ca}\)
\(=\dfrac{b-c}{a\left(a+b\right)+c\left(a+b\right)}+\dfrac{c-a}{b\left(a+b\right)+c\left(a+b\right)}+\dfrac{a-b}{c\left(c+a\right)+b\left(a+c\right)}\)
\(=\dfrac{b-c}{\left(a+c\right)\left(a+b\right)}+\dfrac{c-a}{\left(b+c\right)\left(a+b\right)}+\dfrac{a-b}{\left(b+c\right)\left(a+c\right)}\)
\(=\dfrac{\left(b-c\right)\left(b+c\right)+\left(c-a\right)\left(a+c\right)+\left(a-b\right)\left(a+b\right)}{\left(a+c\right)\left(a+b\right)\left(b+c\right)}\)
\(=\dfrac{b^2-c^2+c^2-a^2+a^2-b^2}{\left(a+b\right)\left(b+c\right)\left(c+a\right)}=0\)

\(b,B=\dfrac{x-4+2\sqrt{x}+6-3\sqrt{x}-4}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}\\ B=\dfrac{x-\sqrt{x}+2}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}=\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}=\dfrac{\sqrt{x}+1}{\sqrt{x}+3}\\ c,M=B:A=\dfrac{\sqrt{x}+1}{\sqrt{x}+3}\cdot\dfrac{\sqrt{x}+3}{x-\sqrt{x}+2}=\dfrac{\sqrt{x}+1}{x-\sqrt{x}+2}\\ M=\dfrac{x-\sqrt{x}+2-x+2\sqrt{x}-1}{x-\sqrt{x}+2}\\ M=1-\dfrac{x-2\sqrt{x}+1}{x-\sqrt{x}+2}=1-\dfrac{\left(\sqrt{x}-1\right)^2}{x-\sqrt{x}+2}\)
Ta có \(\left(\sqrt{x}-1\right)^2\ge0;x-\sqrt{x}+2=\left(\sqrt{x}-\dfrac{1}{2}\right)^2+\dfrac{7}{4}>0\)
Do đó \(\dfrac{\left(\sqrt{x}-1\right)^2}{x-\sqrt{x}+2}\ge0\)
\(\Leftrightarrow M=1-\dfrac{\left(\sqrt{x}-1\right)^2}{x-\sqrt{x}+2}\le1-0=1\)
Vậy \(M_{max}=1\Leftrightarrow\sqrt{x}=1\Leftrightarrow x=1\left(tm\right)\)
a: Thay \(x=3+2\sqrt{2}\) vào A, ta được:
\(A=\dfrac{3+2\sqrt{2}-\sqrt{2}-1+2}{\sqrt{2}+1+3}=\dfrac{4+\sqrt{2}}{4+\sqrt{2}}=1\)

a: Xét ΔABC có góc A+góc B+góc C=180 độ
=>góc A=180 độ-30 độ-20 độ=130 độ
Xét ΔABC có BC/sinA=AC/sinB=AB/sinC
=>AC/sin30=AB/sin20=30/sin130
=>\(AC\simeq19,58\left(cm\right);AB\simeq13,39\left(cm\right)\)
ΔAHB vuông tại H có sin B=AH/AB
=>AH/13,39=1/2
=>AH=6,695(cm)
b: Xét ΔABC có AD là phân giác
nên AB/AC=BD/DC
=>\(\dfrac{BD}{DC}=\dfrac{13.39}{19.58}\)
=>\(\dfrac{BD}{13.39}=\dfrac{CD}{19.58}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{BD}{13.39}=\dfrac{CD}{19.58}=\dfrac{BD+CD}{13.39+19.58}=\dfrac{30}{32.97}=\dfrac{1000}{1099}\)
=>\(BD\simeq12,18\left(cm\right);CD\simeq17,82\left(cm\right)\)

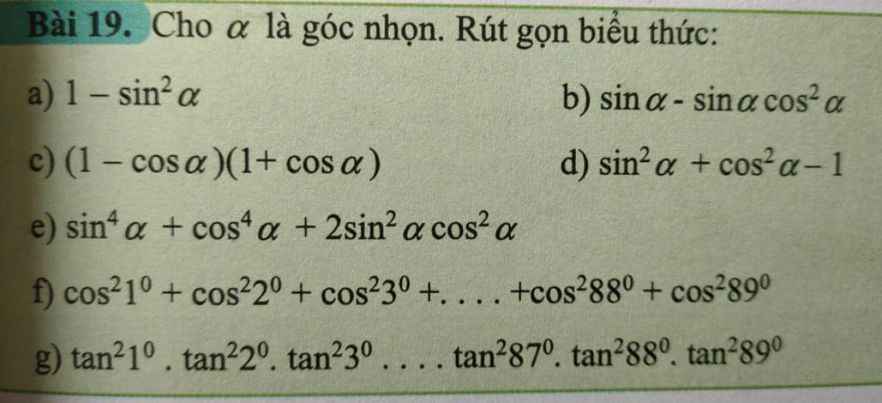 Giải chi tiết giúp a b c
Giải chi tiết giúp a b c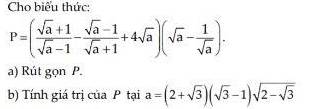



 Giải chi tiết giúp
Giải chi tiết giúp
Lưu ý: \(1=sin^2a+cos^2a\)
Do đó:
a.
\(1-sin^2a=\left(sin^2a+cos^2a\right)-sin^2a=cos^2a\)
b.
\(sina-sina.cos^2a=sina\left(1-cos^2a\right)=sina\left(sin^2a+cos^2a-cos^2a\right)\)
\(=sina.sin^2a=sin^3a\)
c.
\(\left(1-cosa\right)\left(1+cosa\right)=1-cos^2a=sin^2a+cos^2a-cos^2a=sin^2a\)