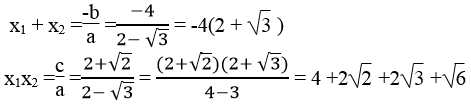NN
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
26 tháng 6 2017
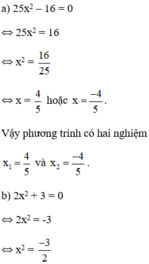
Phương trình vô nghiệm vì x 2 ≥ 0 với mọi x.
c) 4 , 2 x 2 + 5 , 46 x = 0
⇔ x.(4,2x + 5,46) = 0
⇔ x = 0 hoặc 4,2x + 5,46 = 0
+Nếu 4,2x + 5,46 = 0 ⇔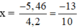 
Vậy phương trình có hai nghiệm
x
1
=
0
và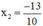 
d) 4 x 2 - 2 √ 3 x = 1 - √ 3 . ⇔ 4 x 2 - 2 √ 3 x – 1 + √ 3 = 0
Có a = 4; b’ = -√3; c = -1 + √3;
Δ ’ = b ' 2 – a c = ( - √ 3 ) 2 – 4 ( - 1 + √ 3 ) = 7 - 4 √ 3 = 4 – 2 . 2 . √ 3 + ( √ 3 ) 2 = ( 2 - √ 3 ) 2 .
Phương trình có hai nghiệm phân biệt:
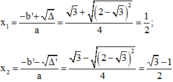
Cách 2: Sử dụng công thức nghiệm thu gọn với a, b, c
Kiến thức áp dụng
Phương trình ax2 + bx + c = 0 (a ≠ 0) có biệt thức Δ = b2 – 4ac.
+ Nếu Δ > 0, phương trình có hai nghiệm phân biệt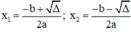 
+ Nếu Δ = 0, phương trình có nghiệm kép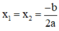 
;
+ Nếu Δ < 0, phương trình vô nghiệm.
CM
20 tháng 7 2019
4,2x2 + 5,46x = 0
⇔ x.(4,2x + 5,46) = 0
⇔ x = 0 hoặc 4,2x + 5,46 = 0
+Nếu 4,2x + 5,46 = 0 ⇔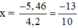 
Vậy phương trình có hai nghiệm x1 = 0 và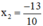 
29 tháng 3 2018
a) Ta có:Δ =(-7)2 -4.2.2 =49 -16 =33 >0
Phương trình có 2 nghiệm phân biệt .Theo hệ thức Vi-ét, ta có:
x1 + x2 =-b/a =7/2 ;x1x2 =c/a =2/2 =1
b) c = -16 suy ra ac < 0
Phương trình có 2 ghiệm phân biệt .Theo hệ thức Vi-ét, ta có:
x1 + x2 =-b/a =-2/5 ;x1x2 =c/a =-16/5
c) Ta có: Δ’ = 22 – (2 -√3 )(2 + √2 ) =4 -4 - 2√2 +2√3 +√6
= 2√3 - 2√2 +√6 >0
Phương trình 2 ghiệm phân biệt .Theo hệ thức Vi-ét, ta có:
d) Ta có : Δ = (-3)2 -4.1,4.1,2 =9 – 6,72 =2,28 >0
Phương trình có 2 ghiệm phân biệt .Theo hệ thức Vi-ét, ta có:
x1 + x2 = -b/a = 3/(1.4) = 30/14 = 15/7 ; x1x2 = c/a = (1.2)/(1.4) = 12/14 = 6/7
Ta có: Δ = 12 -4.5.2 = 1 - 40 = -39 < 0
4 tháng 4 2017
a) 25x2 – 16 = 0 ⇔ 25x2 = 16 ⇔ x2 =
⇔ x = ± = ±
b) 2x2 + 3 = 0: Phương trình vô nghiệm vì vế trái là 2x2 + 3 ≥ 3 còn vế phải bằng 0.
c) 4,2x2 + 5,46x = 0 ⇔ 2x(2,1x + 2,73) = 0
=> x = 0
Hoặc 2,1x + 2,73 = 0 => x = -1,3
d) 4x2 - 2√3x = 1 - √3 ⇔ 4x2 - 2√3x – 1 + √3 = 0
Có a = 4, b = -2√3, b’ = -√3, c = -1 + √3
∆’ = (-√3)2 – 4 . (-1 + √3) = 3 + 4 - 4√3 = (2 - √3)2, √∆’ = 2 - √3
x1 = =
, x2 =
=
4 tháng 3 2021
1) \(4x^2-9=0\)
Theo pt ta có: \(a=4;b=0;c=-9\)
\(\Delta=b^2-4ac=0^2-4.4.\left(-9\right)=144>0\)
=> Pt có 2 nghiệm phân biệt
\(x_1=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{-0-\sqrt{144}}{2.4}=-\dfrac{3}{2}\\ x_2=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{-0+\sqrt{144}}{2.4}=\dfrac{3}{2}\)
2) \(-2x^2+50=0\)
Theo pt ta có: \(a=-2;b=0;c=50\)
\(\Delta b^2-4ac=0^2-4.\left(-2\right).50=400>0\)
=> PT có 2 nghiệm phân biệt
\(x_1=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{-0-\sqrt{400}}{2.\left(-2\right)}=5\\ x_2=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{-0+\sqrt{400}}{2a}=-5\)
3) \(3x^2+11=0\)
Theo pt ta có: \(a=3;b=0;c=11\)
\(\Delta=b^2-4ac=0^2-4.3.11=-132< 0\)
=> PT vô nghiệm
KT
29 tháng 4 2018
a, \(3x^2-2x-5=0\)
\(\Rightarrow\Delta=\left(-2\right)^2-4\times3\times\left(-5\right)\)
\(\Rightarrow\Delta=4+60\)
\(\Rightarrow\Delta=64\)
\(\Rightarrow\sqrt{\Delta}=8\)
vậy phương trình có hai nghiệm phân biệt
\(x_1=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{2+64}{6}=11\)
\(x_2=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{2-64}{6}=\dfrac{-62}{6}=\dfrac{-31}{3}\)
b, \(5x^2+2x-16\)
\(\Rightarrow\Delta=2^2-4\times5\times\left(-16\right)\)
\(\Rightarrow\Delta=4+140\)
\(\Rightarrow\Delta=144\)
\(\Rightarrow\sqrt{\Delta}=12\)
vậyphương trình có hai nghiệm phân biệt
\(x_1=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{-2+12}{10}=\dfrac{10}{10}=1\)
\(x_2=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{-2-12}{10}=\dfrac{-14}{10}=\dfrac{-7}{5}\)
BL
3
17 tháng 7 2016
a)\(\sqrt{2x=0}\)
\(x=0\)
b)\(\sqrt{x=4}\)
\(x=16\)
c)\(\sqrt{3x=\sqrt{9}}\)
\(x=3\)
d)\(-7x=7\)
\(x=-1\)
17 tháng 7 2016
Mình làm vậy có đúng không
Nếu sai bạn sửa cho mình nhé
Cảm ơn