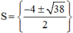Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 1:
Đặt \(\hept{\begin{cases}S=x+y\\P=xy\end{cases}}\) hpt thành:
\(\hept{\begin{cases}S^2-P=3\\S+P=9\end{cases}}\)\(\Leftrightarrow\hept{\begin{cases}S^2-P=3\\S=9-P\end{cases}}\Leftrightarrow\left(9-P\right)^2-P=3\)
\(\Leftrightarrow\orbr{\begin{cases}P=6\Rightarrow S=3\\P=13\Rightarrow S=-4\end{cases}}\).Thay 2 trường hợp S và P vào ta tìm dc
\(\hept{\begin{cases}x=3\\y=0\end{cases}}\)và\(\hept{\begin{cases}x=0\\y=3\end{cases}}\)
Câu 3: ĐK: \(x\ge0\)
Ta thấy \(x-\sqrt{x-1}=0\Rightarrow x=\sqrt{x-1}\Rightarrow x^2-x+1=0\) (Vô lý), vì thế \(x-\sqrt{x-1}\ne0.\)
Khi đó \(pt\Leftrightarrow\frac{3\left[x^2-\left(x-1\right)\right]}{x+\sqrt{x-1}}=x+\sqrt{x-1}\Rightarrow3\left(x-\sqrt{x-1}\right)=x+\sqrt{x-1}\)
\(\Rightarrow2x-4\sqrt{x-1}=0\)
Đặt \(\sqrt{x-1}=t\Rightarrow x=t^2+1\Rightarrow2\left(t^2+1\right)-4t=0\Rightarrow t=1\Rightarrow x=2\left(tm\right)\)

1/ \(\frac{3}{2}x^2+y^2+z^2+yz=1\Leftrightarrow3x^2+2y^2+2z^2+2yz=2\)
\(\Leftrightarrow\left(x^2+y^2+z^2+2xy+2yz+2zx\right)+\left(x^2-2xy+y^2\right)+\left(x^2-2zx+z^2\right)=2\)
\(\Leftrightarrow\left(x+y+z\right)^2+\left(x-y\right)^2+\left(x-z\right)^2=2\)
\(\Rightarrow-\sqrt{2}\le x+y+z\le\sqrt{2}\)
Suy ra MIN A = \(-\sqrt{2}\)khi \(x=y=z=-\frac{\sqrt{2}}{3}\)

a) \(\frac{1}{x-1+\sqrt{x^2-2x+3}}+\frac{1}{x-1-\sqrt{x^2-2x+3}}=1\)
ĐKXĐ : \(x\inℝ\)
\(\Leftrightarrow\frac{x-1-\sqrt{x^2-2x+3}}{\left(x-1+\sqrt{x^2-2x+3}\right)\left(x-1-\sqrt{x^2-2x+3}\right)}+\frac{x-1+\sqrt{x^2-2x+3}}{\left(x-1+\sqrt{x^2-2x+3}\right)\left(x-1-\sqrt{x^2-2x+3}\right)}=\frac{\left(x-1+\sqrt{x^2-2x+3}\right)\left(x-1-\sqrt{x^2-2x+3}\right)}{\left(x-1+\sqrt{x^2-2x+3}\right)\left(x-1-\sqrt{x^2-2x+3}\right)}\)
\(\Rightarrow2x-2=\left[\left(x-1\right)+\left(\sqrt{x^2-2x+3}\right)\right]\left[\left(x-1\right)-\left(\sqrt{x^2-2x+3}\right)\right]\)
\(\Leftrightarrow2x-2=\left(x-1\right)^2-\left(\sqrt{x^2-2x+3}\right)^2\)
\(\Leftrightarrow2x-2=x^2-2x+1-\left(x^2-2x+3\right)\)
\(\Leftrightarrow2x-2=x^2-2x+1-x^2+2x-3\)
\(\Leftrightarrow2x-2=-2\)
\(\Leftrightarrow2x=0\)
\(\Leftrightarrow x=0\)
Vậy phương trình có nghiệm duy nhất x = 0

1.
2. x^2 + 3 = 5y
Hình học hình học:
- Tính chất
Mã mở
hình thức thay thế:
Giải pháp thực sự:
Mã mở
Dung dịch:
- Giải pháp từng bước
Mã mở
Dẫn xuất tiềm ẩn:
- Hơn


a, tìm trong nâng cao phát triển tập 2
b,
ta thấy VT là 1 tam thức bậc 2 nên ta đặt \(\sqrt{\frac{x+3}{2}}=ay+b\)
<=>x+3=2a2y2+4aby+2b2
<=>ax+3a=2a3y2+4a2by+2ab2
<=>ax+3a-2ab2=2a3y2+4a2by
\(\Leftrightarrow\hept{\begin{cases}2x^2+4x=ay+b\\2a^3y^2+4a^2by=ax+3a-2ab^2\end{cases}}\)
đưa hệ này về hệ đối xứng thì ta có:\(\hept{\begin{cases}a^3=1\\a^2b=1\end{cases}\Leftrightarrow\hept{\begin{cases}a=1\\b=1\end{cases}}}\)
\(\Rightarrow\sqrt{2x-1}=y+1\)
sau đó đưa về hệ đối xứng là được
Trên tia đối tia CB lấy F sao cho AM = 2CF
\(\Delta DCF\approx\Delta DAM\left(c-g-c\right)\)
\(\Rightarrow DM=2DF\) và \(\widehat{ADM}=\widehat{CDF}\) nên \(\widehat{MDF}=90^0\) hay \(\Rightarrow\widehat{EDF}+\widehat{MDE}=90^0\) (1)
Lại có \(\widehat{DEC}+\widehat{EDC}=90^0\) \(\Rightarrow\widehat{DEC}+\widehat{MDE}=90^0\) (2)
(1), (2) => \(\widehat{EDF}=\widehat{DEC}\) nên DF = EF
Lại có \(DM=2DF=2EF=2CF+2EC=AM+2EC\)
Done!


x3 + 2x2 – (x – 3)2 = (x – 1)(x2 – 2)
⇔ x3 + 2x2 – (x2 – 6x + 9) = x3 – x2 – 2x + 2
⇔ x3 + 2x2 – x2 + 6x – 9 – x3 + x2 + 2x – 2 = 0
⇔ 2x2 + 8x – 11 = 0.
Có a = 2; b = 8; c = -11 ⇒ Δ’ = 42 – 2.(-11) = 38 > 0
⇒ Phương trình có hai nghiệm:
Vậy phương trình có tập nghiệm