
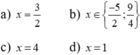
a)
2...">
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời. a) 7x - 35 = 0 <=> 7x = 0 + 35 <=> 7x = 35 <=> x = 5 b) 4x - x - 18 = 0 <=> 3x - 18 = 0 <=> 3x = 0 + 18 <=> 3x = 18 <=> x = 5 c) x - 6 = 8 - x <=> x - 6 + x = 8 <=> 2x - 6 = 8 <=> 2x = 8 + 6 <=> 2x = 14 <=> x = 7 d) 48 - 5x = 39 - 2x <=> 48 - 5x + 2x = 39 <=> 48 - 3x = 39 <=> -3x = 39 - 48 <=> -3x = -9 <=> x = 3 1. Trong các phương trình sau, phương trình bậc nhất 1 ẩn là A. 2/x - 7=0; B. |7x+5)-1=0; C. 8x-9=0 2. điều kiện xác định của phương trình \(\frac{4}{2x-3}=\frac{7}{3x-5}\)là A. x khác 3/2. B. x khác5/3; C. x khác 3/2 hoặc 5/3; D. x khác 3/2 và 5/3 1.Pt bậc nhất 1 ẩn:\(8x-9=0\) 2.ĐKXĐ:\(x\ne\frac{3}{2};x\ne\frac{5}{3}\) Nhìn sơ qua thì thấy bài 3, b thay -2 vào x rồi giải bình thường tìm m Bài 2: a) \(x+x^2=0\) \(\Leftrightarrow x\left(x+1\right)=0\) \(\Leftrightarrow\hept{\begin{cases}x=0\\x+1=0\end{cases}}\)\(\Leftrightarrow\hept{\begin{cases}x=0\\x=0-1\end{cases}}\)\(\Leftrightarrow\hept{\begin{cases}x=0\\x=-1\end{cases}}\) b) \(0x-3=0\) \(\Leftrightarrow0x=3\) \(\Rightarrow vonghiem\) c) \(3y=0\) \(\Leftrightarrow y=0\) a) đặt \(\left(x^2+x\right)\)là \(y\) ta có: \(3y^2-7y+4\)\(=0\) <=>\(\left(3y-4\right)\left(y-1\right)=0\) còn lại bạn tự xử nhé a)\(2+\frac{3}{x-5}=1\) \(\Rightarrow\frac{3}{x-5}=-1\) \(\Rightarrow3=-x+5\) \(\Leftrightarrow x+3=5\) \(\Rightarrow x=2\) a) 2x^2 + 3 = 2x(x + 4) - 7 <=> 2x^2 + 3 = 2x^2 + 8x - 7 <=> 2x^2 - 2x^2 - 8x = - 7 - 3 <=> -8x = -10 <=> x = -10/-8 = 5/4 b) 4x^2 - 12x + 5 = 0 <=> 4x^2 - 2x - 10x + 5 = 0 <=> 2x(2x - 1) - 5(2x - 1) = 0 <=> (2x - 5)(2x - 1) = 0 <=> 2x - 5 = 0 hoặc 2x - 1 = 0 <=> x = 5/2 hoặc x = 1/2 c) |5 - 2x| = 1 - x +) nếu x >= 5/2, ta có: 5 - 2x = 1 - x <=> -2x + 1 = 1 - 5 <=> -x = -4 <=> x = 4 (tm) +) nếu x < 5/2, ta có: -(5 - 2x) = 1 - x <=> -5 + 2x = 1 - x <=> 2x + 1 = 1 + 5 <=> 3x = 6 <=> x = 2 (ktm) d) \(\frac{2}{x-1}=\frac{\left(2x-1\right)\left(2x+1\right)}{x^3-1}-\frac{2x+3}{x^2+x+1}\) ; ĐKXĐ: x # 1 <=> \(\frac{2}{x-1}=\frac{\left(2x-1\right)\left(2x+1\right)}{\left(x-1\right)\left(x^2+x+1\right)}-\frac{2x+3}{x^2+x+1}\) <=> \(\frac{2\left(x^2+x+1\right)}{\left(x-1\right)\left(x^2+x+1\right)}=\frac{\left(2x-1\right)\left(2x+1\right)}{\left(x-1\right)\left(x^2+x+1\right)}-\frac{\left(2x+3\right)\left(x-1\right)}{\left(x-1\right)\left(x^2+x+1\right)}\) <=> 2(x^2 + x + 1) = (2x - 1)(2x + 1) - (2x + 3)(x - 1) <=> 2x^2 + 2x + 2 = 2x^2 - x + 2 <=> 2x^2 - 2x^2 + 2x - x = 2 - 2 <=> x = 0 mạn phép vô đây để kiếm câu trả lời \(2x^2+3=2x\left(x+4\right)-7\) \(< =>2x^2+3=2x.x+4.2x-7\) \(< =>2x^2+3=2x^2+8x-7\) \(< =>2x^2+3-2x^2=8x-7\) \(< =>\left(2x^2-2x^2\right)-8x=-7-3\) \(< =>-8x=-10< =>8x=10\) \(< =>x=10:8=\frac{10}{8}=\frac{5}{4}\) \(a,2x\left(x-3\right)+5\left(x-3\right)=0\) \(\Leftrightarrow\left(2x+5\right)\left(x-3\right)=0\) \(\Leftrightarrow\orbr{\begin{cases}2x+5=0\\x-3=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}2x=-5\\x=3\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=-\frac{5}{2}\\x=3\end{cases}}\) Vậy ......... \(b,\left(x^2-4\right)+\left(x-2\right)\left(3-2x=0\right)\) \(\Leftrightarrow x^2-4-2x^2+7x-6=0\) \(\Leftrightarrow-x^2+7x-10=0\) \(\Leftrightarrow-\left(x-5\right)\left(x-2\right)=0\) \(\Leftrightarrow\orbr{\begin{cases}x=5\\x=2\end{cases}}\) Vậy .................. \(c,x^3-3x^2+3x-1=0\) \(\Leftrightarrow\left(x-1\right)^3=0\) \(\Leftrightarrow x=1\) \(d,x\left(2x-7\right)-4x+14=0\) \(\Leftrightarrow2x^2-7x-4x+14=0\) \(\Leftrightarrow2x^2-11x+14=0\) \(\Leftrightarrow\left(2x-7\right)\left(x-2\right)=0\) \(\Leftrightarrow\orbr{\begin{cases}x=\frac{7}{2}\\x=2\end{cases}}\) Vậy ............ \(e,\left(2x-5\right)^2-\left(x+2\right)^2=0\) \(\Leftrightarrow4x^2-20x+25-x^2-4x-4=0\) \(\Leftrightarrow3x^2-24x+21=0\) \(\Leftrightarrow3\left(x-7\right)\left(x-1\right)=0\) \(\Leftrightarrow\orbr{\begin{cases}x-7=0\\x-1=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=7\\x=1\end{cases}}\) Vậy ..................... \(f,x^2-x-\left(3x-3\right)=0\) \(\Leftrightarrow x^2-x-3x+3=0\) \(\Leftrightarrow x^2-4x+3=0\) \(\Leftrightarrow\left(x-3\right)\left(x-1\right)=0\) \(\Leftrightarrow\orbr{\begin{cases}x-3=0\\x-1=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=3\\x=1\end{cases}}\) Vậy .............. a)\(\frac{x}{5}+\frac{2x+1}{3}=\frac{x-5}{15}\) \(\frac{3x}{15}+\frac{10x+5}{15}=\frac{x-5}{15}\) \(3x+10x+5=x-5\) \(13x+5-x+5=0\) \(12x=-10\) \(x=-\frac{5}{6}\)
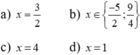






<=> \(\hept{\begin{cases}5-2x\text{ nếu }5-2x\ge0\Leftrightarrow x\ge\frac{5}{2}\\-\left(5-2x\right)\text{ nếu }5-2x< 0\Leftrightarrow x< \frac{5}{2}\end{cases}}\)
