K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
11 tháng 3 2018
a) Bất phương trình đã cho tương đương với hệ sau:
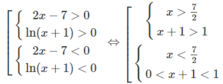
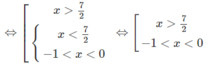
Vậy tập nghiệm là (−1;0) ∪ (7/2; + ∞ )
b) Tương tự câu a), tập nghiệm là (1/10; 5)
c) Đặt t = log 2 x , ta có bất phương trình 2 t 3 + 5 t 2 + t – 2 ≥ 0 hay (t + 2)(2 t 2 + t − 1) ≥ 0 có nghiệm −2 ≤ t ≤ −1 hoặc t ≥ 1/2
Suy ra 1/4 ≤ x ≤ 1/2 hoặc x ≥ 2
Vậy tập nghiệm của bất phương trình đã cho là: [1/4; 1/2] ∪ [ 2 ; + ∞ )
d) Bất phương trình đã cho tương đương với hệ:
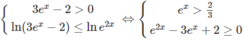
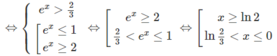
Vậy tập nghiệm là (ln(2/3); 0] ∪ [ln2; + ∞ )
23 tháng 11 2023
1: \(2^x=64\)
=>\(x=log_264=6\)
2: \(2^x\cdot3^x\cdot5^x=7\)
=>\(\left(2\cdot3\cdot5\right)^x=7\)
=>\(30^x=7\)
=>\(x=log_{30}7\)
3: \(4^x+2\cdot2^x-3=0\)
=>\(\left(2^x\right)^2+2\cdot2^x-3=0\)
=>\(\left(2^x\right)^2+3\cdot2^x-2^x-3=0\)
=>\(\left(2^x+3\right)\left(2^x-1\right)=0\)
=>\(2^x-1=0\)
=>\(2^x=1\)
=>x=0
4: \(9^x-4\cdot3^x+3=0\)
=>\(\left(3^x\right)^2-4\cdot3^x+3=0\)
Đặt \(a=3^x\left(a>0\right)\)
Phương trình sẽ trở thành:
\(a^2-4a+3=0\)
=>(a-1)(a-3)=0
=>\(\left[{}\begin{matrix}a-1=0\\a-3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}a=1\left(nhận\right)\\a=3\left(nhận\right)\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}3^x=1\\3^x=3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=0\end{matrix}\right.\)
5: \(3^{2\left(x+1\right)}+3^{x+1}=6\)
=>\(\left[3^{x+1}\right]^2+3^{x+1}-6=0\)
=>\(\left(3^{x+1}\right)^2+3\cdot3^{x+1}-2\cdot3^{x+1}-6=0\)
=>\(3^{x+1}\left(3^{x+1}+3\right)-2\left(3^{x+1}+3\right)=0\)
=>\(\left(3^{x+1}+3\right)\left(3^{x+1}-2\right)=0\)
=>\(3^{x+1}-2=0\)
=>\(3^{x+1}=2\)
=>\(x+1=log_32\)
=>\(x=-1+log_32\)
6: \(\left(2-\sqrt{3}\right)^x+\left(2+\sqrt{3}\right)^x=2\)
=>\(\left(\dfrac{1}{2+\sqrt{3}}\right)^x+\left(2+\sqrt{3}\right)^x=2\)
=>\(\dfrac{1}{\left(2+\sqrt{3}\right)^x}+\left(2+\sqrt{3}\right)^x=2\)
Đặt \(b=\left(2+\sqrt{3}\right)^x\left(b>0\right)\)
Phương trình sẽ trở thành:
\(\dfrac{1}{b}+b=2\)
=>\(b^2+1=2b\)
=>\(b^2-2b+1=0\)
=>(b-1)2=0
=>b-1=0
=>b=1
=>\(\left(2+\sqrt{3}\right)^x=1\)
=>x=0
7: ĐKXĐ: \(x^2+3x>0\)
=>x(x+3)>0
=>\(\left[{}\begin{matrix}x>0\\x< -3\end{matrix}\right.\)
\(log_4\left(x^2+3x\right)=1\)
=>\(x^2+3x=4^1=4\)
=>\(x^2+3x-4=0\)
=>(x+4)(x-1)=0
=>\(\left[{}\begin{matrix}x+4=0\\x-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\left(nhận\right)\\x=-4\left(nhận\right)\end{matrix}\right.\)
Q
7 tháng 6 2017
a) \(2^{x+4}+2^{x+2}=5^{x+1}+3\cdot5^x\)
\(\Rightarrow2^x+2^4+2x^x+2^2=5^x\cdot x+3\cdot5^x\)
\(\Leftrightarrow2^x+16+2^x\cdot4=5\cdot5^x+3\cdot5^x\)
\(\Leftrightarrow16\cdot2^x+4\cdot2^x=8\cdot5^x\)
\(\Leftrightarrow20\cdot2^x=8\cdot5^x\)
\(\Leftrightarrow20\cdot\left(\dfrac{2}{5}\right)^x=8\)
\(\Leftrightarrow\left(\dfrac{2}{5}\right)^x=\dfrac{2}{5}\)
\(\Leftrightarrow\left(\dfrac{2}{5}\right)^x=\left(\dfrac{2}{5}\right)^1\)
\(\Rightarrow x=1\)
PT
1
CM
18 tháng 9 2017
Ta nhận thấy x = 3 là nghiệm của phương trình. Mặt khác, hàm số
Là tổng của hai hàm số mũ với cơ số lớn hơn 1 (hai hàm số đồng biến) nên f(x) đồng biến trên R. Do đó, x = 3 là nghiệm duy nhất của phương trình.
PT
1
CM
15 tháng 8 2018
Bất phương trình đã cho tương đương với hệ sau:
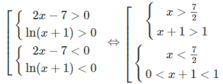
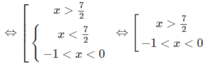
Vậy tập nghiệm là (−1;0) ∪ (7/2; + ∞ )
PT
1
CM
29 tháng 10 2018
(7 - 3i)z + (2 + 3i) = (5 - 4i).z
⇔ [(7 – 3i) – (5 – 4i)].z = - (2 + 3i)
⇔ (2 + i).z = -(2 + 3i)
PT
1
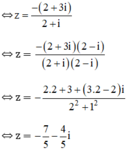
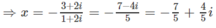
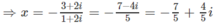
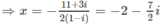
Logarit hóa hai vế theo cơ số 7, ta được:
x 2 + 2 x . log 7 5 − 1 = 0