
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

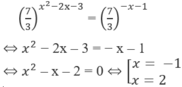

d) Đưa 2 vế về cùng cơ số 2, ta được
\(2^{-3}.2^{4x-6}=\left(2^{\frac{-5}{2}}\right)^x\) hay \(2^{4x-9}=2^{\frac{5}{2}x}\)
Do đó :
\(4x-9=\frac{5}{2}x\Leftrightarrow\frac{3}{2}x=9\Leftrightarrow x=6\)
Vậy phương trình đã cho chỉ có 1 nghiệm x=6
c) Phương trình đã cho tương đương với :
\(\frac{1}{4}.4^x+16.4^x=10\Leftrightarrow\frac{33}{2}.4^x=10\Leftrightarrow4^x=\frac{20}{33}\Leftrightarrow x=\log_4\frac{20}{33}\)
Vậy nghiệm của phương trình là \(x=\log_4\frac{20}{33}\)

a) Chia 2 vế của phương trình cho \(5^x>0\), ta có :
\(\left(\frac{3}{5}\right)^x+\left(\frac{4}{5}\right)^x=1\)
Xét \(f\left(x\right)=\left(\frac{3}{5}\right)^x+\left(\frac{4}{5}\right)^x\)
Ta có :
\(f'\left(x\right)=\left(\frac{3}{5}\right)^x\ln\frac{3}{5}+\left(\frac{4}{5}\right)^x\ln\frac{4}{5}<0\) với mọi x
Do đó \(f\left(x\right)\) đồng biến trên R
Mặt khác
f(2) =1. Do đó x=2 là nghiệm duy nhất của phương trình
b) Phương trình tương đương với
\(2^x\left(2-2^x\right)=x-1\)
Với x=1 thì phương trình trên đúng, do đó x=1 là nghiệm của phương trình
- Nếu x>1 thì \(2<2^x\) và \(x-1>0\) do đó \(2^x\left(2-2^x\right)<0\)< \(x-1\)
phương trình vô nghiệm
- Nếu x<1 thì \(2>2^x\) và \(x-1<0\) do đó \(2^x\left(2-2^x\right)>0\)> \(x-1\)
phương trình đã cho có 1 nghiệm duy nhất là x=1

Đặt \(f\left(x\right)=\left(\frac{1}{6}\right)^x+2\left(\frac{1}{3}\right)^x+3\left(\frac{1}{2}\right)^x\)
Nhận thấy f(2) = 1. Mặt khác f(x) là tổng của các hàm số nghịch biến trên R. Do đó f(x) cũng là hàm nghịch biến. Từ đó ta có :
\(f\left(x\right)<1=f\left(2\right)\Leftrightarrow x>2\)
Vậy tập nghiệm của bất phương trình là
\(D=\left(2;+\infty\right)\)

Từ phương trình thứ nhất ta có : \(y=x-2\)
Thay vào phương trình thứ 2, ta được :
\(3^{x^2+x-2}=3^{-2}\)
Do đó
\(x^2+x-2=-2\) nên \(x=0\) hoặc \(x=-1\)
Suy ra \(y=-2\) hoặc \(y=-3\)
Vậy hệ có 2 nghiệm là \(\left(0;-2\right)\) và \(\left(-1;-3\right)\)

d) Phương trình đã cho tương đương với :
\(2^{3x}+2^x.3^{2x}=2.3^{2x}\Leftrightarrow\left(\frac{2}{3}\right)^{2x}+\left(\frac{2}{3}\right)^x-2=0\)
Đặt \(t=\left(\frac{2}{3}\right)^x,\left(t>0\right)\) Phương trình trở thành
\(t^3+t-2=0\) hay \(\left(t-1\right)\left(t^2+t+2\right)=0\)
Do \(t^2+t+2=\left(t+\frac{1}{2}\right)^2+\frac{7}{4}>0\) nên \(t-1=0\) hay t=1
Từ đó suy ra \(\left(\frac{2}{3}\right)^x=1=\left(\frac{2}{3}\right)^0\Leftrightarrow x=0\)
Vậy phương trình có nghiệm duy nhất \(x=0\)
c) Điều kiện \(x\ne0\). Chia cả 2 vế của phương trình cho \(6^{\frac{1}{x}}>0\), ta có :
\(6.\left(\frac{3}{2}\right)^{\frac{1}{x}}-13.1+6\left(\frac{2}{3}\right)^{\frac{1}{x}}=0\)
Đặt \(t=\left(\frac{3}{2}\right)^{\frac{1}{x}},\left(t>0\right)\)
Phương trình trở thành
\(6t-13+\frac{6}{t}=0\) hay \(6t^2-13t+6=0\)
Phương trình bậc 2 trên có 2 nghiệm dương \(t=\frac{3}{2},t=\frac{2}{3}\)
Với \(t=\frac{3}{2}\) thì \(\left(\frac{3}{2}\right)^{\frac{1}{x}}=\frac{3}{2}\Leftrightarrow\frac{1}{x}=1\Leftrightarrow x=1\)
Với \(t=\frac{2}{3}\) thì \(\left(\frac{3}{2}\right)^{\frac{1}{x}}=\frac{2}{3}\Leftrightarrow\frac{1}{x}=-1\Leftrightarrow x=-1\)