Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a/ \(\sqrt{x-1}+\sqrt{4x-4}-\sqrt{25x-25}+2=0\) (ĐKXĐ : \(x\ge1\))
\(\Leftrightarrow\sqrt{x-1}+2\sqrt{x-1}-5\sqrt{x-1}+2=0\)
\(\Leftrightarrow2\sqrt{x-1}=2\Leftrightarrow x-1=1\Leftrightarrow x=2\)
b/ \(\sqrt{9x^2+18}+2\sqrt{x^2+2}-\sqrt{25x^2+50}+3=0\)
\(\Leftrightarrow3\sqrt{x^2+2}+2\sqrt{x^2+2}-5\sqrt{x^2+2}+3=0\)
<=> 3 = 0 (vô lý)
=> pt vô nghiệm.
c/ \(\frac{9x-7}{\sqrt{7x+5}}=\sqrt{7x+5}\) (ĐKXĐ : x>-5/7)
\(\Leftrightarrow9x-7=7x+5\Leftrightarrow2x=12\Leftrightarrow x=6\)
d/ \(\frac{\sqrt{2x-3}}{\sqrt{x-1}}=2\) (ĐKXĐ : \(x\ge\frac{3}{2}\))
\(\Leftrightarrow2x-3=4\left(x-1\Leftrightarrow\right)2x=1\Leftrightarrow x=\frac{1}{2}\) (loại)
Vậy pt vô nghiệm.
a.
\(\sqrt{4x^2+4x+1}-\sqrt{25x^2+10x+1}=0\)
\(\Leftrightarrow\sqrt{\left(2x+1\right)^2}-\sqrt{\left(5x+1\right)^2}=0\)
\(\Leftrightarrow2x+1-\left(5x+1\right)=0\)
\(\Leftrightarrow-3x=0\Leftrightarrow x=0\)
b.
\(\sqrt{x^4-16x^2+64}=\sqrt{25x^2+10x+1}\)
\(\Leftrightarrow\sqrt{\left(x^2-8\right)^2}=\sqrt{\left(5x+1\right)^2}\)
\(\Leftrightarrow x^2-8=5x+1\)
\(\Leftrightarrow x^2-5x+\dfrac{25}{4}=\dfrac{61}{4}\)
\(\Leftrightarrow\left(x-\dfrac{5}{2}\right)^2=\dfrac{61}{4}\)
............................
tương tự ..
c: \(\Leftrightarrow\sqrt{x-5}\left(\sqrt{x+5}-1\right)=0\)
=>x-5=0 hoặc x+5=1
=>x=-4 hoặc x=5
d: \(\Leftrightarrow\sqrt{2x+3}\left(\sqrt{2x-3}-2\right)=0\)
=>2x+3=0 hoặc 2x-3=4
=>x=7/2 hoặc x=-3/2
e: \(\Leftrightarrow\sqrt{x-2}\left(1-3\sqrt{x+2}\right)=0\)
=>x-2=0 hoặc 3 căn x+2=1
=>x=2 hoặc x+2=1/9
=>x=-17/9 hoặc x=2
a) x=49
b) x=4
c) x = 2 hoặc x = -2
d) x= 11,17355372
e) x =10
f) x=2
g)x = 10 000 000 ( nếu theo đề của bạn) và x=0,94 ( nếu theo đề bđ)
h) x =4
k) x = 4/3 hoặc x = -2/3
l) x = 2,5
m) x = 0,5
n) x=-0,5
Giải PT
a) \(3\sqrt{9x}+\sqrt{25x}-\sqrt{4x} = 3\)
\(\Leftrightarrow\) \(3.3\sqrt{x} +5\sqrt{x} - 2\sqrt{x} = 3 \)
\(\Leftrightarrow\) \(9\sqrt{x}+5\sqrt{x}-2\sqrt{x} = 3 \)
\(\Leftrightarrow\) \(12\sqrt{x} = 3\)
\(\Leftrightarrow\) \(\sqrt{x} = 4 \)
\(\Leftrightarrow\) \(\sqrt{x^2} = 4^2\)
\(\Leftrightarrow\) \(x=16\)
b) \(\sqrt{x^2-2x-1} - 3 =0\)
\(\Leftrightarrow\) \(\sqrt{(x-1)^2} -3=0\)
\(\Leftrightarrow\) \(|x-1|=3\)
* \(x-1=3\)
\(\Leftrightarrow\) \(x=4\)
* \(-x-1=3\)
\(\Leftrightarrow\) \(-x=4\)
\(\Leftrightarrow\) \(x=-4\)
c) \(\sqrt{4x^2+4x+1} - x = 3\)
<=> \(\sqrt{(2x+1)^2} = 3+x\)
<=> \(|2x+1|=3+x\)
* \(2x+1=3+x\)
<=> \(2x-x=3-1\)
<=> \(x=2\)
* \(-2x+1=3+x\)
<=> \(-2x-x = 3-1\)
<=> \(-3x=2\)
<=> \(x=\dfrac{-2}{3}\)
d) \(\sqrt{x-1} = x-3\)
<=> \(\sqrt{(x-1)^2} = (x-3)^2\)
<=> \(|x-1| = x^2-2.x.3+3^2\)
<=> \(|x-1| = x-6x+9\)
<=> \(|x-1| = -5x+9\)
* \(x-1= -5x+9\)
<=> \(x+5x = 9+1\)
<=> \(6x=10\)
<=> \(x= \dfrac{10}{6} =\dfrac{5}{3}\)
* \(-x-1 = -5x+9\)
<=> \(-x+5x = 9+1\)
<=> \(4x = 10\)
<=> \(x= \dfrac{10}{4} = \dfrac{5}{2}\)
a/ ĐK: \(x \ge -1\). Đặt \(\sqrt{x+1}=a \ge 0\)
PT: \(\Leftrightarrow6a-3a-2a=5\)
\(\Leftrightarrow a=5\)
\(\Leftrightarrow x+1=15\Leftrightarrow x=24\) (nhận)
b,c: Hai ý này đều làm theo cách bình phương hoặc đưa về phương trình chứa dấu giá trị tuyệt đối được nhé.
b) Cách 1: ĐKXĐ: Tự tìm
\(\sqrt{x^{2}-4x+4}=2\Leftrightarrow x^{2}-4x+4=4\Leftrightarrow x(x-4)=0\)
\(\Leftrightarrow x=0\) hoặc \(x=4\) cả 2 cái này đều TMĐK
Cách 2: \((\sqrt{x^2-4x+4}=2)\)
\(\Leftrightarrow \sqrt{(x-2)^2}=2\)
\(\Leftrightarrow \mid x-2\mid=2\)
Với \(x\geq 2\) thì :
\(x-2=2 \Leftrightarrow x=4\) (nhận)
Với \(x<2\) thì
\(-x-2=2\Leftrightarrow x=0\) (nhận)
Vậy \(S={0;4}\)
c) Cách 1: \(\sqrt{x^{2}-6x+9}=x-2\Leftrightarrow \left\{\begin{matrix}x\geq 2 \\ x^{2}-6x+9=x^{2}-4x+4 \end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix}x\geq 2 \\ x=\frac{5}{2} \end{matrix}\right.\)
Nghiệm TMĐK
Cách 2: \((\sqrt{x^2-6x+9}=x-2)\)
\(\Leftrightarrow \mid x-3\mid =x-2\)
Với \(x\geq 3\) thì
\(x-3=x-2\Leftrightarrow 0x=-1\) ( vô lý)
Với \(x<3\) thì
\(-x+3=x-2\Leftrightarrow -2x=-5 \Leftrightarrow x=\frac{5}{2}\)
Vậy \(S={\frac{5}{2}}\)
d) ĐKXĐ: Tự tìm
\(\sqrt{x^{2}+4}=\sqrt{2x+3}\Leftrightarrow x^{2}+4=2x+3\Leftrightarrow x^{2}-2x+1=0\Leftrightarrow (x-1)^{2}=0\)
\(\Leftrightarrow x=1\)
e) ĐKXĐ: \(x\geq \frac{3}{2}\)
\(\frac{\sqrt{2x-3}}{\sqrt{x-1}}=2\Leftrightarrow \frac{2x-3}{x-1}=4\Rightarrow 2x-3=4x-4\Leftrightarrow x=\frac{1}{2}\)
Nghiệm không TMĐK.
Phương trình vô nghiệm.
f) ĐKXĐ: \(x\geq \frac{-15}{2}\)
\(x+\sqrt{2x+15}=0\Leftrightarrow 2x+2\sqrt{2x+15}=0\Leftrightarrow 2x+15+2\sqrt{2x+15}+1-16=0\)
\(\Leftrightarrow (\sqrt{2x+15}+1)^{2}-4^{2}=0\Leftrightarrow (\sqrt{2x+15}+5)(\sqrt{2x+15}-3)=0\)
\(\Leftrightarrow \sqrt{2x+15}-3=0\Leftrightarrow \sqrt{2x+15}=3\Leftrightarrow 2x+15=9\Leftrightarrow x=-3\) (TMĐK)
\(a,\frac{3x+2}{\sqrt{x+2}}=2\sqrt{x+2}\)
\(\Rightarrow3x+2=2\sqrt{x+2}.\sqrt{x+2}\)
\(\Rightarrow3x+2=2\left(x+2\right)\)
\(\Rightarrow3x+2=2x+4\)
\(\Rightarrow3x-2x=4-2\)
\(\Rightarrow x=2\)
\(b,\sqrt{4x^2-1}-2\sqrt{2x+1}=0\)
\(\Rightarrow\sqrt{\left(2x+1\right)\left(2x-1\right)}-2\sqrt{2x+1}=0\)
\(\Rightarrow\sqrt{2x+1}\left(\sqrt{2x-1}-2\right)=0\)
\(\Rightarrow\hept{\begin{cases}\sqrt{2x+1}=0\\\sqrt{2x-1}-2=0\end{cases}\Rightarrow\orbr{\begin{cases}2x+1=0\\\sqrt{2x-1}=2\end{cases}\Rightarrow}\orbr{\begin{cases}2x=-1\\2x-1=4\end{cases}\Rightarrow}\orbr{\begin{cases}x=-\frac{1}{2}\\2x=5\end{cases}\Rightarrow}\orbr{\begin{cases}x=-\frac{1}{2}\\x=\frac{5}{2}\end{cases}}}\)
\(c,\sqrt{x-2}+\sqrt{4x-8}-\frac{2}{5}\sqrt{\frac{25x-50}{4}}=4\)
\(\Rightarrow\sqrt{x-2}+\sqrt{4\left(x-2\right)}-\frac{2}{5}\sqrt{\frac{25\left(x-2\right)}{4}}=4\)
\(\Rightarrow\sqrt{x-2}+2\sqrt{x-2}-\frac{2}{5}.\frac{5\sqrt{x-2}}{2}=4\)
\(\Rightarrow\sqrt{x-2}+2\sqrt{x-2}-\sqrt{x-2}=4\)
\(\Rightarrow2\sqrt{x-2}=4\)
\(\Rightarrow\sqrt{x-2}=2\)
\(\Rightarrow x-2=4\)
\(\Rightarrow x=6\)
\(d,\sqrt{x+4}-\sqrt{1-x}=\sqrt{1-2x}\)
\(\Rightarrow\sqrt{x+4}=\sqrt{1-2x}+\sqrt{1-x}\)
\(\Rightarrow x+4=1-2x+2\sqrt{\left(1-2x\right)\left(1-x\right)}+1-x\)
\(\Rightarrow x+4=2-3x+2\sqrt{1-3x+2x^2}\)
\(\Rightarrow x+4-2+3x=2\sqrt{1-3x+2x^2}\)
\(\Rightarrow4x+2=2\sqrt{1-3x+2x^2}\)
\(\Rightarrow2x+1=\sqrt{1-3x+2x^2}\)
\(\Rightarrow4x^2+4x+1=1-3x+2x^2\)
\(\Rightarrow4x^2-2x^2+4x+3x+1-1=0\)
\(\Rightarrow2x^2+7x=0\)
\(\Rightarrow x\left(2x+7\right)=0\)
\(\Rightarrow\orbr{\begin{cases}x=0\\2x+7=0\end{cases}\Rightarrow\orbr{\begin{cases}x=0\\x=\frac{-7}{2}\end{cases}}}\)
\(e,\frac{2x}{\sqrt{5}-\sqrt{3}}-\frac{2x}{\sqrt{3}+1}=\sqrt{5}+1\)
\(\frac{2x\left(\sqrt{5}+\sqrt{3}\right)}{5-3}-\frac{2x\left(\sqrt{3}-1\right)}{3-1}=\sqrt{5}+1\)
\(\Rightarrow x\left(\sqrt{5}+\sqrt{3}\right)-x\left(\sqrt{3}-1\right)=\sqrt{5}+1\)
\(\Rightarrow\sqrt{5}x+\sqrt{3}x-\sqrt{3x}+x=\sqrt{5}+1\)
\(\Rightarrow\sqrt{5}x+x=\sqrt{5}+1\)
\(\Rightarrow x\left(\sqrt{5}+1\right)=\sqrt{5}+1\)
\(\Rightarrow x=1\)
\(\sqrt{25x^2-10x+1}=4x+9\)
\(\Leftrightarrow\sqrt{\left(5x-1\right)^2}=4x+9\)
\(\Leftrightarrow\left|5x-1\right|=4x+9\)
\(\Leftrightarrow\orbr{\begin{cases}5x-1=4x+9\\5x-1=-4x-9\end{cases}\Leftrightarrow\orbr{\begin{cases}x=10\\x=-\frac{8}{9}\end{cases}}}\)
Vậy ...
\(\sqrt{x^2+2x+1}=\sqrt{x+1}\)
\(\Leftrightarrow\sqrt{\left(x+1\right)^2}=\sqrt{x+1}\)
\(\Leftrightarrow\sqrt{\left(x+1\right)^2}-\sqrt{x+1}=0\)
\(\Leftrightarrow\sqrt{x+1}.\left(\sqrt{x+1}-1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}\sqrt{x+1}=0\\\sqrt{x+1}-1=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=-1\\x=0\end{cases}}}\)
Vậy ...
a) đkxđ: \(\begin{cases}\sqrt{x^2-4}\ge0\\\sqrt{x^2}+4x+4\ge0\end{cases}\) \(\Leftrightarrow\begin{cases}\begin{cases}x-2\ge0\\x+2\ge0\end{cases}\\x+2\ge0\end{cases}\) \(\Leftrightarrow\begin{cases}x\ge2\\x\le-2\end{cases}\) \(\Leftrightarrow-2\ge x\ge2\)
\(\sqrt{x^2-4}+\sqrt{x^2+4x+4}=0\)
\(\Leftrightarrow\sqrt{\left(x-2\right)\left(x+2\right)}+\sqrt{\left(x+2\right)^2}=0\)
\(\Leftrightarrow\sqrt{\left(x-2\right)\left(x+2\right)}=x+2\)
\(\Leftrightarrow\left(x-2\right)\left(x+2\right)=\left(x+2\right)^2\)
\(\Leftrightarrow\left(x+2\right)\left(x-2-x+2\right)=0\)
\(\Leftrightarrow x+2=0\)
\(\Leftrightarrow x=-2\)
S={-2}
b) đkxđ: \(\begin{cases}\sqrt{1-x^2}\ge0\\\sqrt{x+1}\ge0\end{cases}\) \(\Leftrightarrow\begin{cases}1-x^2\ge0\\x+1\ge0\end{cases}\) \(\Leftrightarrow\begin{cases}x^2\le1\\x\ge-1\end{cases}\) \(\Leftrightarrow\begin{cases}\begin{cases}x\le1\\x\ge-1\end{cases}\\x\ge-1\end{cases}\) \(\Leftrightarrow-1\le x\le1\)
\(\sqrt{1-x^2}+\sqrt{x+1}=0\)
\(\Leftrightarrow\sqrt{1-x^2}=-\sqrt{x+1}\)
\(\Leftrightarrow1-x^2=x+1\)
\(\Leftrightarrow-x-x^2=0\)
\(\Leftrightarrow-x\left(1+x\right)=0\)
\(\Leftrightarrow\left[\begin{array}{nghiempt}-x=0\\1+x=0\end{array}\right.\) \(\Leftrightarrow\left[\begin{array}{nghiempt}x=0\left(N\right)\\x=-1\left(N\right)\end{array}\right.\)
S={-1;0}
a) \(\sqrt{x^2-6x+9}=3\)
⇔ \(\sqrt{\left(x-3\right)^2}=3\)
⇔ \(\left|x-3\right|=3\)
⇔ \(\orbr{\begin{cases}x-3=3\\x-3=-3\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=6\\x=0\end{cases}}\)
b) \(\sqrt{x^2-8x+16}=x+2\)
⇔ \(\sqrt{\left(x-4\right)^2}=x+2\)
⇔ \(\left|x-4\right|=x+2\)
⇔ \(\orbr{\begin{cases}x-4=x+2\left(x\ge4\right)\\4-x=x+2\left(x< 4\right)\end{cases}\Leftrightarrow}x=1\)
c) \(\sqrt{x^2+6x+9}=3x-6\)
⇔ \(\sqrt{\left(x+3\right)^2}=3x-6\)
⇔ \(\left|x-3\right|=3x-6\)
⇔ \(\orbr{\begin{cases}x-3=3x-6\left(x\ge3\right)\\3-x=3x-6\left(x< 3\right)\end{cases}}\Leftrightarrow x=\frac{9}{4}\)
d) \(\sqrt{x^2-4x+4}-2x+5=0\)
⇔ \(\sqrt{\left(x-2\right)^2}-2x+5=0\)
⇔ \(\left|x-2\right|-2x+5=0\)
⇔ \(\orbr{\begin{cases}x-2-2x+5=0\left(x\ge2\right)\\2-x-2x+5=0\left(x< 2\right)\end{cases}}\Leftrightarrow x=3\)
a) 25x2 – 16 = 0 ⇔ 25x2 = 16 ⇔ x2 =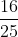
⇔ x = ±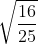
= ±
b) 2x2 + 3 = 0: Phương trình vô nghiệm vì vế trái là 2x2 + 3 ≥ 3 còn vế phải bằng 0.
c) 4,2x2 + 5,46x = 0 ⇔ 2x(2,1x + 2,73) = 0
=> x = 0
Hoặc 2,1x + 2,73 = 0 => x = -1,3
d) 4x2 - 2√3x = 1 - √3 ⇔ 4x2 - 2√3x – 1 + √3 = 0
Có a = 4, b = -2√3, b’ = -√3, c = -1 + √3
∆’ = (-√3)2 – 4 . (-1 + √3) = 3 + 4 - 4√3 = (2 - √3)2, √∆’ = 2 - √3
x1 =
= 
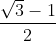, x2 = 
= 