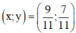Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

phương trình đầu tương đương với:
\(x\left(x^2+y^2\right)=y^4\left(y^2+1\right)\)
\(\Leftrightarrow x^3+xy^2-y^6-y^4=0\)
\(\Leftrightarrow\left(x^3-y^6\right)+\left(xy^2-y^4\right)=0\)
\(\Leftrightarrow\left(x-y^2\right)\left(x^2+xy^2+y^4\right)+y^2\left(x-y^2\right)=0\)
\(\Leftrightarrow\left(x-y^2\right)\left(x^2+xy^2+y^4+y^2\right)=0\)
TH1: \(x-y^2=0\Rightarrow x=y^2\) thay vào pt thứ hai ta tìm được nghiệm
\(\sqrt{4y^2+5}+\sqrt{y^2+8}=6\)
\(4y^2+5+y^2+8+2\sqrt{\left(4y^2+5\right)\left(y^2+8\right)}=36\)
\(5y^2+13+2\sqrt{\left(4y^2+5\right)\left(y^2+8\right)}=36\)
\(2\sqrt{\left(4y^2+5\right)\left(y^2+8\right)}=23-5y^2\)
bình phương hai vế tiếp rồi đưa về pt trùng phương, bạn tự giải tiếp nhé
TH2: \(x^2+xy^2+y^4+y^2=0\), coi x là ẩn, tìm x theo y ta có
\(\Delta=y^4-4\left(y^4+y^2\right)=-3y^4-y^2\)
Pt có nghiệm khi y =0, thay vào ta có từ pt thứ nhất suy ra x =0, nhưng pt thứ hai không thỏa mãn

Đối với casio 580 VNX bấm \(Mode\rightarrow9\rightarrow1\rightarrow2\)
a) - Đối với máy casio 570 VN Plus / 570 ES Plus : bấm \(Mode\rightarrow5\rightarrow1\) . Nhập các hệ số : \(a_1=\frac{3}{4};b_1=-\frac{7}{3};c_1=\frac{4}{5};a_2=\frac{2}{5};b_2=\frac{2}{7};c_2=\frac{2}{9}\)
\(\Rightarrow\left\{{}\begin{matrix}x=\frac{1412}{2169}\\y=-\frac{161}{1205}\end{matrix}\right.\)
b) \(\left\{{}\begin{matrix}x=-\frac{913}{1064}\\y=\frac{167}{1064}\end{matrix}\right.\)

\(\text{Condition}:x,y\ge0\)
\(\hept{\begin{cases}x^2+2x=4-\sqrt{y}\left(M_1\right)\\y^2+2y=4-\sqrt{x}\left(M_2\right)\end{cases}}\)
\(\left(M_1\right)-\left(M_2\right)\Leftrightarrow\left(x^2-y^2\right)+2\left(x-y\right)+\left(\sqrt{x}-\sqrt{y}\right)=0\)
\(\Leftrightarrow\left(x+y\right)\left(\sqrt{x}+\sqrt{y}\right)\left(\sqrt{x}-\sqrt{y}\right)+2\left(\sqrt{x}+\sqrt{y}\right)\left(\sqrt{x}-\sqrt{y}\right)+\left(\sqrt{x}-\sqrt{y}\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=y\\\left(x+y\right)\left(\sqrt{x}+\sqrt{y}\right)+2\left(\sqrt{x}+\sqrt{y}\right)+1=0\left(M_3\right)\end{cases}}\)
x=0 khong phai nghiem PT\(\Rightarrow M_3\)(fail)
Thay x=y vao
:D

a) Cả hai phương trình đều có chung \(\sqrt{x+3}\)
pt đầu suy ra \(\sqrt{x+3}=2\sqrt{y-1}\)
pt sau suy ra \(\sqrt{x+3}=4-\sqrt{y+1}\)
Vậy \(2\sqrt{y-1}=4-\sqrt{y+1}\), đk y > 1
\(4\left(y-1\right)=16-8\sqrt{y+1}+y+1\)
\(8\sqrt{y+1}+3y-21=0\)
Đặt \(\sqrt{y+1}=t\)
=> y = t2 - 1
=> 8t + 3(t2 -1) -21 =0
3t2 + 8t - 24 = 0
=> t = ...
=> y = t2 - 1
=> \(\sqrt{x+3}=2\sqrt{y-1}\)
=> x =...
b) Trừ hai pt cho nhau ta có:
x2 - y2 = 3(y - x)
(x - y) (x + y + 3) = 0
=> x = y hoặc x + y + 3 = 0
Xét hai trường hợp, rút x theo y rồi thay trở lại một trong hai pt ban đầu tìm ra nghiệm

ĐKXĐ: ....
\(\Leftrightarrow\left\{{}\begin{matrix}\frac{5}{x-2}-2-\frac{2}{y-3}=2\\1+\frac{4}{x-2}-\frac{2}{y-3}=4\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}\frac{5}{x-2}-\frac{2}{y-3}=4\\\frac{4}{x-2}-\frac{2}{y-3}=3\end{matrix}\right.\)
\(\Rightarrow\frac{1}{x-2}=1\Rightarrow x-2=1\Rightarrow x=3\)
\(\Rightarrow\frac{2}{y-3}=\frac{5}{x-2}-4=1\Rightarrow y-3=2\Rightarrow y=5\)
Nghiệm của hệ \(\left(x;y\right)=\left(3;5\right)\)
Vậy hệ phương trình có nghiệm