Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) và b) Chứng minh nhờ tính chất đường trung bình của tam giác
c) Để chứng minh MNQR là ngũ giác đều ta cần chứng minh hai điều : Hình đó có tất cả các cạnh bằng nhau và có tất cả các góc bằng nhau.

Do ABCD là hình vuông có M, N, P, Q lần lượt là trung điểm của BC, CD, DA, AB nên: AQ = QB = BM = MC= CN = ND = DP = PA
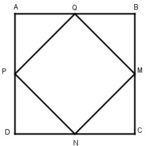
Xét Δ APQ và Δ BQM:
AQ = BM (gt)
∠ A = ∠ B = 90 0
AP = BQ (gt)
Do đó: △ APQ = △ BQM (c.g.c) ⇒ PQ = QM (1)
Xét △ BQM và △ CMN:
BM = CN (gt)
∠ B = ∠ C = 90 0
BQ = CM (gt)
Do đó: △ BQM = △ CMN (c.g.c) ⇒ QM = MN (2)
Xét △ CMN và △ DNP:
CN = DP (gt)
∠ C = ∠ D = 90 0
CM = DN (gt)
Do đó: △ CMN = △ DNP (c.g.c) ⇒ MN = NP (3)
Từ (1), (2) và (3) suy ra: MN = NP = PQ = QM
nên tứ giác MNPQ là hình thoi
Vì AP = AQ nên △ APQ vuông cân tại A
BQ = BM nên △ BMQ vuông cân tại B
⇒ ∠ (AQP) = ∠ (BQM) = 45 0
∠ (AQP) + ∠ (PQM) + ∠ (BQM) = 180 0 (kề bù)
⇒ ∠ (PQM) = 180 0 - ( ∠ (AQP) + ∠ (BQM) )
= 180 0 - ( 45 0 + 45 0 ) = 90 0
Vậy tứ giác MNPQ là hình vuông.

1)Xét tam giác PSQ có PD=DS(gt),PA=AQ(gt)
=>DA là đường trung bình của tam giác PSQ
=>DA//SQ,DA=1/2SQ(1)
Xét tam giác RSQ có RC=CS(gt),RB=BQ(gt)
=>CB là đường trung bình của tam giác RSQ
=>CB//SQ,CB=1/2SQ(2)
Từ (1) và (2)=> DA//CB,DA=CB
=>ABCD là hình bình hành(3)
Xét tam giác SPR coSD=DP(gt),SC=CR(gt)
=>DC là đường trung bình của tam giác SPR
=>DC//PR
Ta có PR vuông góc với SQ(gt)
Mà SQ//DA(cmt)
=>PR vuông góc với DA
Mặt khác DC//PR(cmt)
=>DC vuông góc với DA hay góc ADC=90(4)
Từ (3) và (4)=>ABCD là hình chứ nhật
2)
Xét tam giác BAC có BU=UA(gt), BV=VC(gt)
=>UV là đường trung bình của tam giác BAC
=>UV//AC, UV=1/2AC (1)
Xét tam giác DAC có DZ=ZA(gt),DT=TC(gt)
=>ZT là đường trung bình của tam giác DAC
=>ZT//AC, ZT=1/2AC (2)
Từ (1) và (2) => UV//ZT, UV=ZT
=>UVTZ là hình bình hành(3)
Xét tam giác ABD có AZ=ZD(gt),AU=UB(gt)
=>UZ là đường trung bình của tam giác ABD
=>UZ//BD, UZ=1/2BD
Ta có BD vuông góc với AC(gt)
Mà UV//AC
=>BD vuông góc với UV
Mà UZ//BD(cmt)
=> UZ vuông góc với UV hay góc VUZ=90(4)
Từ (3) và (4)=> UVTZ là hình chữ nhật(5)
Mặt khác UV=1/2AC(cmt), UZ=1/2BD
Mà AC=BD
=>UV=UZ(6)
Từ (5) và (6)=>UVTZ là hình vuông
 Nga Phạm
Nga Phạm

1. bn tự viết gt kl nha
E D G H N M Q P
Xét tam giác MEN và tam giác PGN, có :
ME=PG( gt)
góc MEN=goc PGN (=90 độ)
EN=NG(gt)
DO đó tam giác MEN =tam giác PGN (c.g.c)
suy ra MN=PN(hai cạnh tương ứng) (1)
Ta được :
PN=QP(2)
PQ=QM(3)
QM=MN(4)
Từ (1) (2) (3) (4) suy ra MN=PN=QP=MQ
Vậy MNPQ là hình thoi.
Chúc bạn học tốt![]()
2. bn tự vẽ hình và gt kl lun nha
Xét tam giác PSQ, có
PD=DS(gt),PA=AQ(gt)
=>DA là đường trung bình của tam giác PSQ
=>DA//SQ,DA=1/2SQ(1)
Xét tam giác RSQ, có
RC=CS(gt),RB=BQ(gt)
=>CB là đường trung bình của tam giác RSQ
=>CB//SQ,CB=\(\dfrac{1}{2}\)SQ(2)
Từ (1) và (2)=> DA//CB,DA=CB
=>ABCD là hình bình hành(3)
Xét tam giác SPR, có
SD=DP(gt)
SC=CR(gt)
=>DC là đường trung bình của tam giác SPR
=>DC//PR
Ta có:
PR vuông góc với SQ(gt)
Mà SQ//DA(cmt)
=>PR vuông góc với DA
Mặt khác DC//PR(cmt)
=>DC vuông góc với DA hay góc ADC=90(4)
Từ (3) và (4)=>ABCD là hình chữ nhật.
Chúc bạn học tốt![]()

a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)

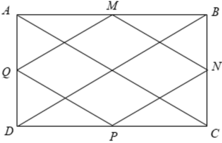
M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, AD
⇒ AM = MB; BN = NC; CP = DP; AQ = DQ
+ Xét Δ ABD có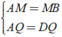
⇒ MQ là đường trung bình của Δ ABD.
⇒ QM = 1/2BD = 1/2AC ( 1 )
+ Xét Δ ABC có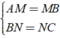
⇒ MN là đường trung bình của Δ ABC.
⇒ MN = 1/2BD = 1/2AC ( 2 )
+ Xét Δ BCD có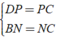
⇒ NP là đường trung bình của Δ BCD.
⇒ NP = 1/2BD = 1/2AC ( 3 )
+ Xét Δ ADC có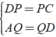
⇒ QP là đường trung bình của Δ ADC.
⇒ QP = 1/2BD = 1/2AC ( 4 )
Từ ( 1 ),( 2 ),( 3 ),( 4 ) ⇒ MN = NP = PQ = QM.
⇒ MNPQ là hình thoi.
xét tam giác MEN và tam giác PGN co :
ME=PG( giả thiết)
góc MEN=goc PGN (=90 độ)
EN=NG(GIẢ THIẾT)
DO đó tam giác MEN =tam giác PGN (c.g.c)
suy ra MN=PN(hai cạnh tương ứng) 1
Ta được :
PN=QP(2)
PQ=QM(3)
QM=MN(4)
Từ (1) (2) (3) (4) suy ra MN=PN=QP=MQ
Vậy MNPQ là hình thoi
nhớ tick đúng cho mình với nha cảm ơn mấy bạn