Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: \(\dfrac{x-1}{3}-\dfrac{3x+5}{2}\ge1-\dfrac{4x+5}{6}\)
\(\Leftrightarrow2\left(x-1\right)-3\left(3x+5\right)\ge6-4x-5\)
\(\Leftrightarrow2x-2-9x-15-6+4x+5\ge0\)
\(\Leftrightarrow-3x\ge18\)
hay \(x\le-6\)

a: =>2x<=-8
=>x<=-4
b: =>x+5<0
=>x<-5
c: =>2x>8
=>x>4
d: =>3x>=9
=>x>=3

\(x-\frac{2}{4}-\frac{2}{3}\ge5x-\frac{9}{12}\)
\(\Leftrightarrow x-\frac{7}{6}\ge5x-\frac{3}{4}\)
\(\Leftrightarrow-4x\ge\frac{5}{12}\)
\(\Leftrightarrow-\frac{5}{56}\ge x\)

\(\frac{x+4}{5}+\frac{3x+2}{10}< \frac{x-1}{3}\)
\(\Leftrightarrow\frac{6\left(x+4\right)}{30}+\frac{3\left(3x+2\right)}{30}< \frac{10\left(x-1\right)}{30}\)
\(\Leftrightarrow6x+24+9x+6< 10x-10\)
\(\Leftrightarrow5x+40< 0\)
\(\Leftrightarrow x< -8\)
Tự biểu diễn nha bạn
\(\frac{x+4}{5}+\frac{3x+2}{10}< \frac{x-1}{3}\)
\(\Rightarrow\frac{6\left(x+4\right)}{30}+\frac{3\left(3x+2\right)}{30}< \frac{10\left(x-1\right)}{30}\)
\(\Rightarrow6x+24+9x+6< 10x-10\)
\(5x< -40\)
\(\Rightarrow x< -8\)

A, 3X+6>0
(=)3X>-6
(=)X>-2
VẬY ...
B,10-2X≥-4
(=)-2X≥-4-10
(=)-2X≥-14
(=)X≤7
VẬY....
C,
(=)
(=) -15X+10>-3+3X
(=)-15X-3X>-3-10
(=)-18X>-13
(=)X<

`(x+4)/5 - (x-2)/3 > 2`
`=> (3x+12 - 5x + 10)/15 > 2`
`=> 24 - 2x > 30`
`=> -2x > 6`
`=> x < -3`.

x + x - 1/2 > x - 2/3
<=> 2x - 1/2 > x - 2/3
<=> x > -1/6
x/3 + 3x - 4/5 >= 2x - 3
<=> 4x/3 >= -11/5
<=> 4x >= -33/5
<=> x >= -33/20
Tập nghiệm chung của 2 bất phương trình là : x >-1/6

1:
a: =>3x=6
=>x=2
b: =>4x=16
=>x=4
c: =>4x-6=9-x
=>5x=15
=>x=3
d: =>7x-12=x+6
=>6x=18
=>x=3
2:
a: =>2x<=-8
=>x<=-4
b: =>x+5<0
=>x<-5
c: =>2x>8
=>x>4


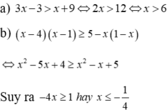
⇔ 2x - 2 - 9x - 15 ≥ 6 - 4x - 5
⇔ 2x - 9x + 4x ≥ 6 - 5 + 2 + 15
⇔ -3x ≥ 18
⇔ x ≤ -6
Vậy tập nghiệm của phương trình là S= {x|x ≤ -6}
Biểu diễn nghiệm trên trục số: