
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Biểu diễn số học sinh làm được bài I, bài II, bài III bằng biểu đồ Ven

Vì chỉ có 1 học sinh giải đúng 3 bài nên điền số 1 vào phần chung của 3 hình tròn.
Có 2 học sinh giải được bài I và bài II, nên phần chung của 2 hình tròn này mà không chung với hình tròn khác sẽ điền số 1 (vì 2- 1 = 1).
Tương tự, ta điền được các số 4 và 5 (trong hình).
Nhìn vào hình vẽ ta có:
+ Số học sinh chỉ làm được bài I là: 20 – 1 – 1 – 5 = 13 (bạn)
+ Số học sinh chỉ làm được bài II là: 14 – 1 – 1 – 4 = 8 (bạn)
+ Số học sinh chỉ làm được bài III là: 10 – 5 – 1 – 4 = 0 (bạn)
Vậy số học sinh làm được ít nhất một bài là: (Cộng các phần không giao nhau trong hình)
13 + 1 + 8 + 5 + 1 + 4 + 0 = 32 (bạn)
Suy ra số học sinh không làm được bài nào là:
35 – 32 = 3 (bạn)
Đáp số: 3 bạn





a^2 + 4b^2 - 16 + 4ab
= (a^2 +4ab +4b^2)-16
= (a+2b)^2 -4^2
=(a+2b-4)(a+2b+4)
:v, nhìn đề muốn mỏi mắt, bắt đầu từ câu 1 tự luận hả bạn

gọi a,b,c lần lượt là số học sinh chỉ giải được bài A,B,C
d là số học sinh giải được 2 bài B và C nhưng không giải được bài A
Khi đó : số học sinh giải được bài A và thêm ít nhất 1 bài trong hai bài B và C là : 25 - a - b - c - d
Theo bài ra :
Số thí sinh chỉ giải được bài A bằng số thí sinh chỉ giải được bài B cộng với số thí sinh chỉ giải được bài C
\(\Rightarrow a=b+c\)
số thí sinh không giải được bài A thì số thí sinh đã giải được bài B gấp hai lần số học sinh giải được bài C
\(\Rightarrow b+d=2\left(c+d\right)\)
Số học sinh chỉ giải được bài A nhiều hơn số thí sinh giải được bài A và thêm bài khác là một người
\(\Rightarrow\) a = 1 + 25 - a - b - c - d
từ các đẳng thức trên suy ra : \(\hept{\begin{cases}b=2c+d\\3\left(b+c\right)=26-d\end{cases}\Rightarrow\hept{\begin{cases}d=b-2c>0\\3\left(b+c\right)+b-2c=26\end{cases}}}\)
\(\Rightarrow\hept{\begin{cases}d=b-2c>0\\4b+c=26\end{cases}\Rightarrow\hept{\begin{cases}b=6\\c=2\end{cases}}}\)
Vậy ....

\(\left(\frac{1}{2}xy-1\right).\left(x^3-2x-6\right)=\frac{1}{2}xy.\left(x^3-2x-6\right)+\left(-1\right).\left(x^3-2x-6\right)\)
= \(\frac{1}{2}xy.x^3+\frac{1}{2}xy.\left(-2x\right)+\frac{1}{2xy}.\left(-6\right)+\left(-1\right).x^3+\left(-1\right).\left(-2x\right)+\left(-1\right).\left(-6\right)\)
= \(\frac{1}{2}x^{\left(1+3\right)}y-x^{\left(1+1\right)}y-3xy-x^3+2x+6\)
= \(\frac{1}{2}x^4y-x^2y-3xy-x^3+2x+6\)
= \(\frac{1}{2}x^4y-x^3-x^2y-3xy+2x+6\)
Chúc bạn học tốt !!!
Bài làm
Ta có: ( xy - 1 )( x3 - 2x - 6 )
= ( xy . x3 ) + [ xy . ( -2x ) ] + [ xy . ( - 6 ) ] + [ ( -1 ) . x3 ] + [ ( -1 ) . ( -2x ) ] + [ ( -1 ) . ( -6 ) ] ( * chỗ này nếu thầnh thạo phép nnhân đa thức r thì k cần pk ghi đâu )
= x4y - 2x2y - 6xy - x3 + 2x + 6
# Học tốt #




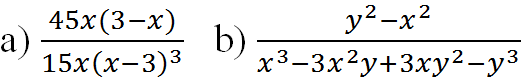


 giải hôk
giải hôk xy – 1 với đa thức x3 – 2x – 6.
xy – 1 với đa thức x3 – 2x – 6.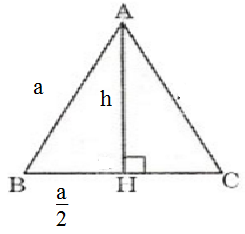
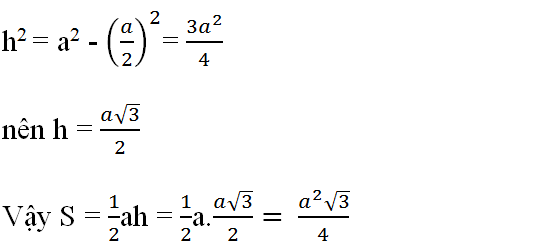
\(\frac{x}{x+1}-\frac{2x-3}{1-x}=\frac{3x^2+5}{x^2-1}\)ĐK : \(x\ne\pm1\)
\(\Leftrightarrow\frac{x}{x+1}+\frac{2x-3}{x-1}=\frac{3x^2+5}{x^2-1}\)
\(\Leftrightarrow\frac{x\left(x-1\right)}{\left(x-1\right)\left(x+1\right)}+\frac{\left(2x-3\right)\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}=\frac{3x^2+5}{\left(x-1\right)\left(x+1\right)}\)
\(\Rightarrow x^2-x+2x^2+2x-3x+3=3x^2+5\)
\(\Leftrightarrow-2x-2=0\Leftrightarrow x=-1\) vô lí
Vậy phương trình vô nghiệm
\(\frac{x}{x+1}-\frac{2x-3}{1-x}=\frac{3x^2+5}{x^2-1}\)
\(\Leftrightarrow\frac{x\left(x-1\right)}{\left(x+1\right)\left(x-1\right)}+\frac{\left(2x-3\right)\left(x+1\right)}{\left(x+1\right)\left(x-1\right)}=\frac{3x^2+5}{\left(x-1\right)\left(x+1\right)}\)
\(\Rightarrow x^2-x+2x^2+2x-3x-3=3x^2+5\)
\(\Leftrightarrow x^2-x+2x^2+2x-3x-3-3x^2-5=0\)
\(\Leftrightarrow-2x-8=0\)
\(\Leftrightarrow-2x=8\)
\(\Leftrightarrow x=-4\)