K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
14 tháng 7 2023
1:
a: Xét tứ giác ABDC có
M là trung điểm chung của AD và BC
=>ABDC là hình bình hành
mà góc BAC=90 độ
nên ABDC là hình chữ nhật
=>AB//CD và AB=CD
b: Xét ΔABC và ΔCDA có
AB=CD
BC=DA
AC chung
=>ΔABC=ΔCDA
c: ΔCBA vuông tại A
mà AM là trung tuyến
nên AM=BC/2
NT
0
10 tháng 3 2022
a: Xét ΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó: ΔABD=ΔEBD
b: Ta có: ΔBAD=ΔBED
nên BA=BE
=>ΔBAE cân tại B
mà \(\widehat{ABE}=60^0\)
nên ΔABE đều
MT
17 tháng 8 2017
ta có: x/2 + 3/y = 5/4
=> 5/4 - x/2 = 3/y
=> 5/4 - 2x/4 = 3/y
=> (5 -2x)/4 = 3/y
=> y(5 - 2x) = 12
Suy ra: y; 5-2x thuộc ước của 12 = 1; -1; 2; -2; 3;-3;4;-4;6;-6;12;-12 (1)
Vì x, y là số nguyên dương nên 2x>0 => 5 - 2x>4
Nên từ (1) suy ra 5-2x = 6;12
Ta có bảng:
| 5-2x | 6 | 12 |
| y | 2 | 1 |
| 2x | -1 | -7 |
| x | không có | không có |
Vậy không có giá trị để x,y thỏa mãn đề bài
17 tháng 8 2017
Ta có : \(\frac{x}{2}+\frac{3}{y}=\frac{5}{4}\)
\(\Rightarrow\frac{5}{4}-\frac{x}{2}=\frac{3}{y}\)
\(\Rightarrow\frac{5}{4}-\frac{2x}{4}=\frac{3}{y}\)
\(\Rightarrow\frac{5-2x}{4}=\frac{3}{y}\)
\(\Rightarrow y\left(5-2x\right)=12\)
\(\Rightarrow\) y = 5 - 2x \(\in\) Ư(12) = { 1 ; -1 ; 2 ; -2 ; 3 ; -3 ; 4 ; -4 ; 6 ; -6 ; 12 ; -12 }
Vì x ; y là số nguyên dương nên 2x > 0 \(\rightarrow\) 5 - 2x > 4
\(\Rightarrow\) 5 - 2x = 6 ; 12 nên ta có bảng sau :
| 5 - 2x | 6 | 12 |
| y | 2 | 1 |
| 2x | -1 | -7 |
| x | không có | không có |
Vậy không có x ; y để thỏa mãn đề bài .
5 tháng 1
a: Xét ΔABD và ΔAMD có
AB=AM
\(\widehat{BAD}=\widehat{MAD}\)
AD chung
Do đó: ΔABD=ΔAMD
b: Ta có: ΔABD=ΔAMD
=>DB=DM
=>ΔDBM cân tại D
c: Ta có: AB=AM
=>A nằm trên đường trung trực của BM(1)
Ta có: DB=DM
=>D nằm trên đường trung trực của BM(2)
Từ (1) và (2) suy ra AD là đường trung trực của BM
PT
giúp mik với ạ mik cần gấp. GIẢI CỤ THỂ GIÚP MIK vs ạ
2
5 tháng 3 2022
Câu 3:
a: \(BD=\sqrt{BC^2-DC^2}=4\left(cm\right)\)
b: \(\widehat{A}=180^0-2\cdot70^0=40^0< \widehat{B}\)
nên BC<AC=AB
c: Xét ΔEBC vuông tại E và ΔDCB vuông tại D có
BC chung
\(\widehat{EBC}=\widehat{DCB}\)
Do đó:ΔEBC=ΔDCB
d: Xét ΔOBC có \(\widehat{OBC}=\widehat{OCB}\)
nên ΔOBC cân tại O
KV
31 tháng 10 2023
Câu 2
a) Thay y = -2 vào biểu thức đã cho ta được:
2.(-2) + 3 = -1
Vậy giá trị của biểu thức đã cho tại y = -2 là -1
b) Thay x = -5 vào biểu thức đã cho ta được:
2.[(-5)² - 5] = 2.(25 - 5) = 2.20 = 40
Vậy giá trị của biểu thức đã cho tại x = -5 là 40
P
3
25 tháng 7 2021
a, Đặt \(x=2k;y=3k\)
Ta có : \(xy=54\Rightarrow6k^2=54\Leftrightarrow k^2=9\Leftrightarrow k=\pm3\)
Với k = 3 thì x = 6 ; y = 9
Với k = -3 thì x = -6 ; y = -9
b, Áp dụng tính chất dãy tỉ số bằng nhau
\(\dfrac{x}{5}=\dfrac{y}{3}=\dfrac{x^2-y^2}{25-9}=\dfrac{4}{16}=\dfrac{1}{4}\Rightarrow x=\dfrac{5}{4};y=\dfrac{3}{4}\)
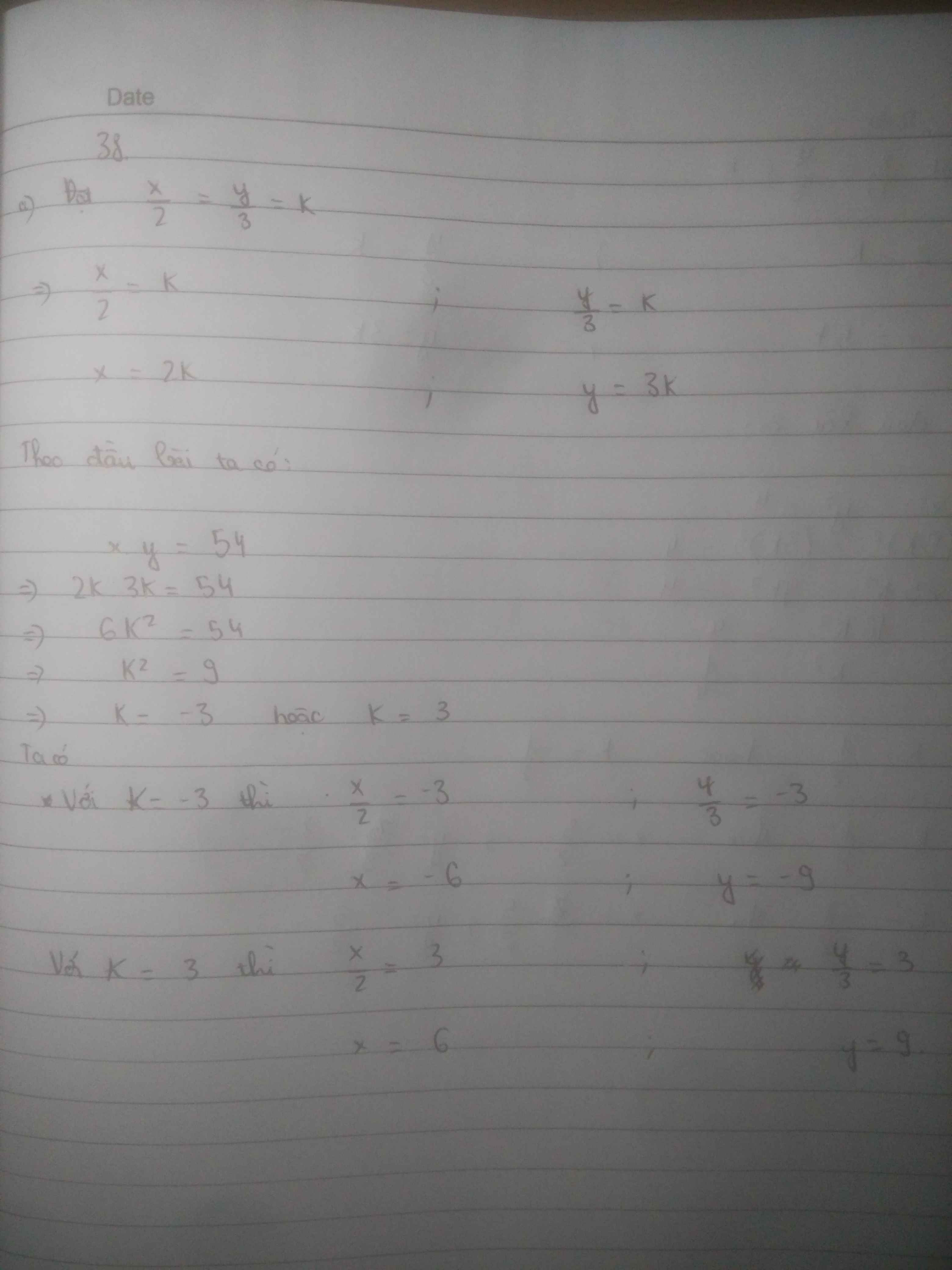
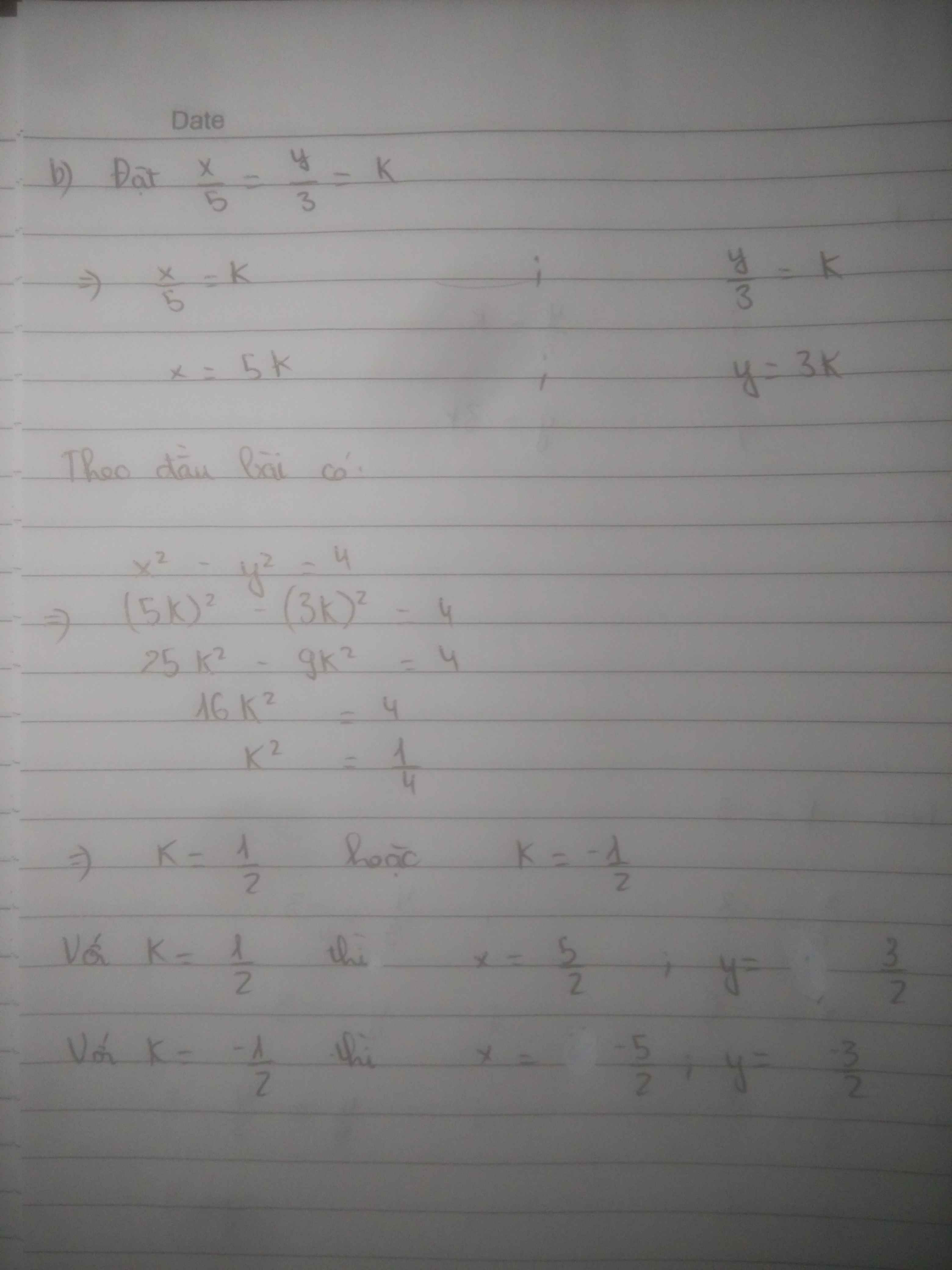
a: Xét ΔMAB và ΔCBA có
\(\widehat{MAB}=\widehat{ABC}\)(hai góc so le trong, MA//BC)
AB chung
\(\widehat{ABM}=\widehat{BAC}\)(hai góc so le trong, MB//AC)
Do đó;ΔMAB=ΔCBA
Xét ΔABC và ΔCNA có
\(\widehat{BAC}=\widehat{NCA}\)(hai góc so le trong, BA//CN)
AC chung
\(\widehat{BCA}=\widehat{NAC}\)(hai góc so le trong, AN//BC)
Do đó: ΔABC=ΔCNA
b: ΔMAB=ΔCBA
=>MA=CB
ΔABC=ΔCNA
=>BC=NA
mà BC=AM
nên AM=AN
mà M,A,N thẳng hàng
nên A là trung điểm của MN