Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hãy tích cho tui đi
khi bạn tích tui
tui không tích lại bạn đâu
THANKS
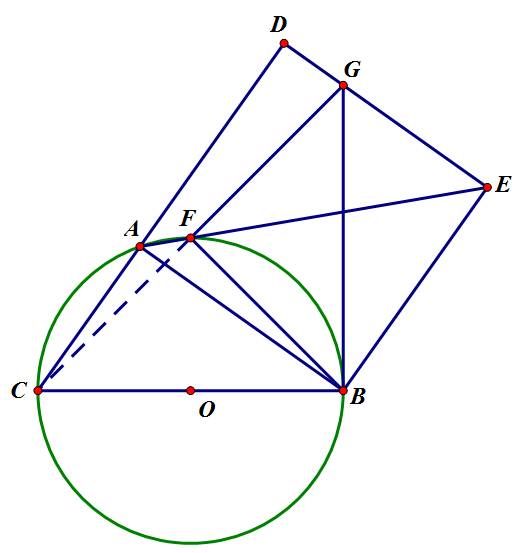
cho đường tròn (o) đường kính AB, gọi C là 1 điểm bất kì trên đường tròn (o) sao cho CA>CB. Vẽ hình vuông ACDE có đỉnh D nằm trên tia đối tia BC, đường chéo CE cắt đường tròn tại F. cmr
a. F là điểm chính giữa cung AB
b. Tam giác ABF vuông cân
c. Tia DE cắt tia BF tại M. Cm 4 điểm A,B,D,M cùng thuộc một đường tròn từ đó suy ra AM là tiếp tuyến của (o)

△ABC nội tiếp đường tròn đường kính BC.
\(\Rightarrow\)△ABC vuông tại A.
- Ta có: \(\widehat{ABC}+\widehat{ABG}=90^0\) (\(BG\perp BC\) tại B).
\(\widehat{EBG}+\widehat{ABG}=90^0\) (\(AB\perp EB\) tại B).
\(\Rightarrow\widehat{ABC}=\widehat{EBG}\)
△ABC và △EBG có: \(\widehat{ABC}=\widehat{EBG}\) (cmt)
\(AB=EB\) (ABED là hình vuông).
\(\widehat{BAC}=\widehat{BEG}=90^0\)
\(\Rightarrow\)△ABC=△EBG (g-c-g).
\(\Rightarrow\widehat{ACB}=\widehat{EGB}\) (1).
AFBC là tứ giác nội tiếp có \(\widehat{EFB}\) là góc ngoài đỉnh F.
\(\Rightarrow\widehat{ACB}=\widehat{EFB}\) (2).
(1), (2) \(\Rightarrow\widehat{EGB}=\widehat{EFB}\) nên GEBF nội tiếp.

1: góc CFG=1/2(sđ cung CB+sđ cung AE)
=1/2(sđ cung AC+sđ cung AE)
=1/2*sđ cung CE
=góc CHE
=>góc CFG=góc CHE
=>180 độ-góc EFG=góc CHE
=>góc EFG+góc EHG=180 độ
=>EFGH nội tiếp

A B C D O E F G H x y I
1/
Ta có
sđ cung AC = sđ cung BC (1)
\(sđ\widehat{CFG}=\dfrac{1}{2}\left(sđcungBC+sđcungAE\right)\) (góc có đỉnh ở trong hình tròn) (2)
\(sđ\widehat{CHE}=\dfrac{1}{2}sđcungCAE=\dfrac{1}{2}\left(sđcungAC+sđcungAE\right)\) (góc nội tiếp) (3)
Từ (1) (2) (3) \(\Rightarrow\widehat{CFG}=\widehat{CHE}\)
Ta có
\(\widehat{CFG}+\widehat{EFG}=\widehat{EFC}=180^o\)
\(\Rightarrow\widehat{CHE}+\widehat{EFG}=180^o\)
=> EFGH là tứ giác nội tiếp (Tứ giác có hai góc đối bù nhau là tứ giác nội tiếp)
2/
sđ cung AC = sđ cung BC (4)
\(sđ\widehat{AGC}=\dfrac{1}{2}\left(sđcungAC+sđcungBH\right)\) (5) (góc có đỉnh ở trong hình tròn)
\(sđ\widehat{CHy}=\dfrac{1}{2}sđcungCBH=\dfrac{1}{2}\left(sđcungBC+sđcungBH\right)\) (6) (Góc giữa tiếp tuyến và dây cung)
Từ (4) (5) (6) \(\Rightarrow\widehat{AGC}=\widehat{CHy}\)
Mà AC = AG (gt) => tgACG cân tại A \(\Rightarrow\widehat{AGC}=\widehat{ACG}\)
\(\Rightarrow\widehat{ACG}=\widehat{CHy}\) mà 2 góc trên ở vị trí so le trong => xy//AC
Đường tròn c: Đường tròn qua C với tâm O Đoạn thẳng f: Đoạn thẳng [B, C] Đoạn thẳng l: Đoạn thẳng [B, A] Đoạn thẳng m: Đoạn thẳng [D, A] Đoạn thẳng n: Đoạn thẳng [B, E] Đoạn thẳng p: Đoạn thẳng [D, E] Đoạn thẳng q: Đoạn thẳng [A, E] Đoạn thẳng a: Đoạn thẳng [C, H] Đoạn thẳng a: Đoạn thẳng [C, H] Đoạn thẳng b: Đoạn thẳng [B, G] Đoạn thẳng e: Đoạn thẳng [E, G] Đoạn thẳng f_1: Đoạn thẳng [C, G] B = (-0.88, 2.62) B = (-0.88, 2.62) B = (-0.88, 2.62) C = (6.04, 2.64) C = (6.04, 2.64) C = (6.04, 2.64) Điểm O: Trung điểm của f Điểm O: Trung điểm của f Điểm O: Trung điểm của f Điểm A: Điểm trên c Điểm A: Điểm trên c Điểm D: Giao điểm của d, g Điểm D: Giao điểm của d, g Điểm D: Giao điểm của d, g Điểm E: Giao điểm của i, j Điểm E: Giao điểm của i, j Điểm E: Giao điểm của i, j Điểm F: Giao điểm của c, k Điểm F: Giao điểm của c, k Điểm F: Giao điểm của c, k Điểm G: Giao điểm của r, s Điểm G: Giao điểm của r, s Điểm G: Giao điểm của r, s Điểm H: Giao điểm của c, n Điểm H: Giao điểm của c, n Điểm H: Giao điểm của c, n
a. Do AE là đường chéo hinh vuông nên \(\widehat{BAE}=\widehat{EAD}\Rightarrow\widehat{BAF}=\widehat{FAC}\)
Chúng lại là hai góc nội tiếp chắn cũng BF và FC nên cung FB = FC.
Vậy dây FB = FC, mà \(\widehat{BFC}=90^o\) (Do BC là đường kính) nên tam giác FBC vuông cân tại F.
b) Do ABED là hình vuông nên AE vuông góc BD tại trung điểm mỗi đường. Vậy tam giác BFD cân tại F hay FB = FD.
Do câu a: FB = FC nên FC = FD.
c) Gọi G là giao điểm của CF và tiếp tuyến tại B của đường tròn đường kính BC. Khi đó G cố định.
Gọi H là giao điểm của BE với đường tròn. Ta thấy ngay ABHC là hình chữ nhật nên AC = BH hay cung AC = cung BH.
Khi đó \(\widehat{GBE}=\widehat{AFC}=\widehat{GFE}\) nên tứ giác BFEG nội tiếp. Suy ra E thuộc đường tròn qua ba điểm B, G, F.
Giải bài toán hình Cho (O) đường kính BC và một điểm A nằm trên cung BC sao cho AB>AC.Trên tia AC lấy điểm D sao cho AD=AB, vẽ hình vuông BADE,tia AE cắt (O) tại điểm thứ hai F. a) chứng minh BGDC nội tiếp HELP ME PLEASE