Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Thời gian cả đi cả về của ca nô là : 11h30p - 7h - 30p = 4h
Gọi vận tốc riêng của ca nô là : x ( x >0 ; km/h)
Vận tốc xuôi dòng là : x +4( km/h)
Vận tốc ngược dòng là : x - 4 ( km/h)
Thời gian lúc đi là : 30:x+4 ( h)
Thời gian lúc về là : 30:x−4 ( h)
Theo đó , ta có phương trình sau :
30:(x+4)+30:(x-4) = 4
⇔ 30( x - 4) + 30( x + 4) = 4( x2 - 16)
⇔ 4x2 - 60x - 64 = 0
⇔ 4x2 + 4x - 64x - 64 = 0
⇔ 4x( x + 1) - 64( x + 1) = 0
⇔ ( x + 1)( 4x - 64) = 0
⇔ x = -1 ( KTM) hoặc x = 16 ( TM)

Đổi 7 giờ 30 phút =15/2 (h)
Gọi vận tốc thực của ca nô là x (km/h), x > 3
Vận tốc của ca nô khi xuôi dòng sông từ A đến B là x + 3 (km/h)
Vận tốc của ca nô khi ngược dòng sông từ B về A là x – 3 (km/h)
Thời gian của ca nô khi xuôi dòng sông từ A đến B là 54/(x+3) (h)
Thời gian của ca nô khi ngược dòng song từ B về A là 54/(x-3) (h)
Do ca nô chạy xuôi dòng từ A đến B rồi chạy ngược dòng từ B về A hết tất cả 7 giờ 30 phút nên ta có phương trình:
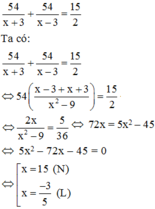
Vậy vận tốc thực của ca nô là 15 (km/h)
Đáp án: D

gọi x (Km/ h)là vận tốc của ca nô khi nước yên lặng
vận tốc khi đi suôi dòng là x + 3
vận tốc khi đi ngực dòng là x - 3
thời gian khi đi suôi dòng là \(\dfrac{30}{x+3}\)
thời gian khi đi ngực dòng là \(\dfrac{30}{x-3}\)
thời gian nghỉ là 40 phút = \(\dfrac{40}{60}\) = \(\dfrac{2}{3}\) giờ
vì tổng thời gian từ lúc đi đến lúc trở về là 6 giờ
nên ta có phương trình :
\(\dfrac{30}{x+3}\)+\(\dfrac{30}{x-3}\)+\(\dfrac{2}{3}\) = 6
\(\Leftrightarrow\) \(\dfrac{30.\left(x-3\right)+30.\left(x+3\right)}{\left(x+3\right)\left(x-3\right)}\) +\(\dfrac{2}{3}\) = 6
\(\Leftrightarrow\) \(\dfrac{60x}{x^2-9}\)+\(\dfrac{2}{3}\) = 6\(\Leftrightarrow\) \(\dfrac{60x}{x^2-9}\)= \(\dfrac{16}{3}\)
\(\Leftrightarrow\) 180x = 16x2 - 144\(\Leftrightarrow\) 16x2 -180x -144 = 0
\(\Leftrightarrow\) 4x2 - 45x -36 = 0
giải \(\Delta\) ta có 2 nghiệm :x1=12 (tmđk) ; x2=-\(\dfrac{3}{4}\) (loại)
vậy vận tốc khi nước yên lặng là 12(Km/h)

Gọi vận tốc thực là x(km/h) x>0
Vận tốc xuôi:x+3(km/h)
Vận tốc ngược:x-3(km/h)
Thời gian đi từ xuôi dòng : \(\dfrac{48}{x+3}\)( h)
Thời gian đi ngược dòng: \(\dfrac{48}{x-3}\)(h)
Theo bài ra ta có pt
\(\dfrac{48}{x-3}\)+\(\dfrac{48}{x+3}\)+\(\dfrac{20}{60}\)=7
Giải ra được x=15(tm)
Vậy....