
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(2M=\frac{3-1}{1.2.3}+\frac{4-2}{2.3.4}+\frac{5-3}{3.4.5}+...+\frac{12-10}{10.11.12}=\)
\(=\frac{1}{1.2}-\frac{1}{2.3}+\frac{1}{2.3}-\frac{1}{3.4}+\frac{1}{3.4}-\frac{1}{4.5}+...+\frac{1}{10.11}-\frac{1}{11.12}=\frac{1}{2}-\frac{1}{11.12}\)
\(\Rightarrow M=\frac{1}{4}-\frac{1}{11.24}=\frac{66-1}{11.24}=\frac{65}{11.24}\)

\(a,\frac{6}{7}+\frac{5}{8}:5-\frac{3}{16}\cdot(-2)^2\)
\(=\frac{6}{7}+\frac{5}{8}:\frac{5}{1}-\frac{3}{16}\cdot4\)
\(=\frac{6}{7}+\frac{5}{8}\cdot\frac{1}{5}-\frac{3}{16}\cdot4\)
\(=\frac{6}{7}+\frac{1}{8}-\frac{3\cdot4}{16}\)
\(=\frac{6}{7}+\frac{1}{8}-\frac{3\cdot1}{4}\)
\(=\frac{6}{7}+\frac{1}{8}-\frac{3}{4}=\frac{48+7-42}{56}=\frac{13}{56}\)
\(b,\frac{2}{3}+\frac{1}{3}\cdot\left[\frac{-2}{3}+\frac{5}{6}\right]:\frac{2}{3}\)
\(=\frac{2}{3}+\frac{1}{3}\cdot\left[\frac{-4+5}{6}\right]:\frac{2}{3}\)
\(=\frac{2}{3}+\frac{1}{3}\cdot\frac{1}{6}:\frac{2}{3}=\frac{2}{3}+\frac{1}{3}\cdot\frac{1}{6}\cdot\frac{3}{2}=\frac{2}{3}+\frac{1}{12}=\frac{8}{12}+\frac{1}{12}=\frac{9}{12}=\frac{3}{4}\)
c, Xem lại đề
d, \(\frac{-3}{5}+\left[\frac{-2}{5}-99\right]\)
\(=\frac{-3}{5}+\frac{-497}{5}=\frac{-500}{5}=-100\)
b, Tìm x
\(\left[\frac{2}{11}+\frac{1}{3}\right]\cdot x=\left[\frac{1}{7}-\frac{1}{8}\right]\cdot56\)
\(\Rightarrow\left[\frac{2}{11}+\frac{1}{3}\right]\cdot x=\left[\frac{8}{56}-\frac{7}{56}\right]\cdot56\)
\(\Rightarrow\left[\frac{6}{33}+\frac{11}{33}\right]\cdot x=1\)
\(\Rightarrow\frac{17}{33}\cdot x=1\)
\(\Rightarrow x=1:\frac{17}{33}=1\cdot\frac{33}{17}=\frac{33}{17}\)


B=1+(2-3-4+5)+(6-7-8+9)+.....................+(298-299-300+301)+302
B=1+302=303

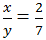
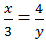
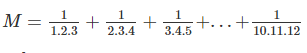
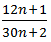 là phân số tối giản (n ∈ N)
là phân số tối giản (n ∈ N)