Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Hệ số biến dạng theo mỗi trục đo O'x', O'y', O'z' lần lượt là:
p=O'A'OA=22=1�=�'�'��=22=1;
q=O'B'OB=13�=�'�'��=13;
r=O'C'OC=46=23�=�'�'��=46=23.

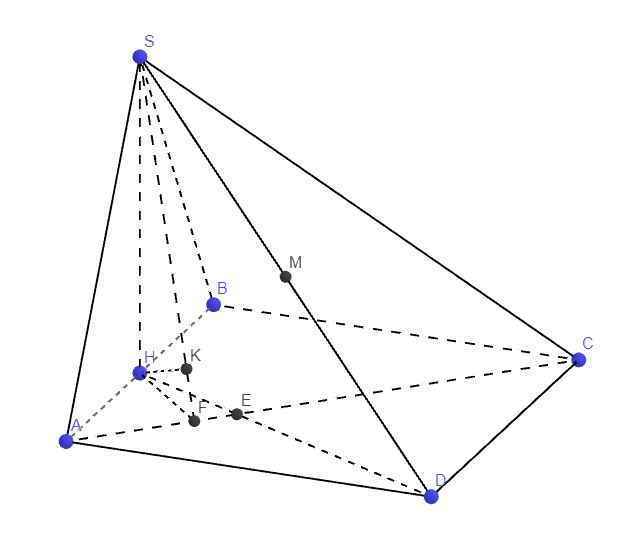
Gọi H là trung điểm AB, có lẽ từ 2 câu trên ta đã phải chứng minh được \(SH\perp\left(ABCD\right)\)
Do \(\left\{{}\begin{matrix}DM\cap\left(SAC\right)=S\\MS=\dfrac{1}{2}DS\end{matrix}\right.\) \(\Rightarrow d\left(M;\left(SAC\right)\right)=\dfrac{1}{2}d\left(D;\left(SAC\right)\right)\)
Gọi E là giao điểm AC và DH
Talet: \(\dfrac{HE}{DE}=\dfrac{AH}{DC}=\dfrac{1}{2}\Rightarrow HE=\dfrac{1}{2}DE\)
\(\left\{{}\begin{matrix}DH\cap\left(SAC\right)=E\\HE=\dfrac{1}{2}DE\end{matrix}\right.\) \(\Rightarrow D\left(H;\left(SAC\right)\right)=\dfrac{1}{2}d\left(D;\left(SAC\right)\right)=d\left(M;\left(SAC\right)\right)\)
Từ H kẻ HF vuông góc AC (F thuộc AC), từ H kẻ \(HK\perp SF\)
\(\Rightarrow HK\perp\left(SAC\right)\Rightarrow HK=d\left(H;\left(SAC\right)\right)\)
ABCD là hình vuông \(\Rightarrow\widehat{HAF}=45^0\Rightarrow HF=AH.sin45^0=\dfrac{a\sqrt{2}}{4}\)
\(SH=\dfrac{a\sqrt{3}}{2}\), hệ thức lượng:
\(HK=\dfrac{SH.HF}{\sqrt{SH^2+HF^2}}=\dfrac{a\sqrt{21}}{14}\)
\(\Rightarrow d\left(M;\left(SAC\right)\right)=\dfrac{a\sqrt{21}}{14}\)

a.
\(sin\left(2x-\dfrac{\pi}{4}\right)=-1\)
\(\Leftrightarrow2x-\dfrac{\pi}{4}=-\dfrac{\pi}{2}+k2\pi\)
\(\Leftrightarrow x=-\dfrac{\pi}{8}+k\pi\) (1)
\(-\dfrac{\pi}{3}\le x\le\dfrac{7\pi}{3}\Rightarrow-\dfrac{\pi}{3}\le-\dfrac{\pi}{8}+k\pi\le\dfrac{7\pi}{3}\)
\(\Rightarrow-\dfrac{5}{24}\le k\le\dfrac{59}{24}\Rightarrow k=\left\{0;1;2\right\}\)
Thế vào (1) \(\Rightarrow x=\left\{-\dfrac{\pi}{8};\dfrac{7\pi}{8};\dfrac{15\pi}{8}\right\}\)

ĐKXĐ: \(-2\le x\le3\)
Đặt \(\sqrt{x+2}+2\sqrt{3-x}=a\Rightarrow4\sqrt{6+x-x^2}-3x=a^2-14\)
Mặt khác \(a^2=\left(\sqrt{x+2}+2\sqrt{3-x}\right)^2\le5\left(x+2+3-x\right)=25\)
\(\Rightarrow a\le5\)
Và \(\sqrt{x+2}+\sqrt{3-x}+\sqrt{3-x}\ge\sqrt{5}+\sqrt{3-x}\ge\sqrt{5}\) \(\Rightarrow a\ge\sqrt{5}\)
\(\Rightarrow\sqrt{5}\le a\le5\)
Phương trình trở thành:
\(a^2-14=ma\Leftrightarrow\frac{a^2-14}{a}=m\) với \(a\in\left[\sqrt{5};5\right]\)
\(f\left(a\right)=\frac{a^2-14}{a}\Rightarrow f'\left(a\right)=\frac{2a^2-a^2+14}{a^2}=\frac{a^2+14}{a^2}>0\)
\(\Rightarrow f\left(a\right)\) đồng biến \(\Rightarrow f\left(\sqrt{5}\right)\le f\left(a\right)\le5\)
\(\Rightarrow-\frac{9\sqrt{5}}{5}\le f\left(a\right)\le\frac{11}{5}\Rightarrow-\frac{9\sqrt{5}}{5}\le m\le\frac{11}{5}\)


Em mới hc lớp 7 thôi không biết đúng không
Có tập hợp A={1;2;3;....;30}
Suy ra số phần tử của tập hợp A là
(30-1)+1=30 (phần tử)
Mà hiệu hai số bất kì không nhỏ hơn 2
Suy ra Hiệu của chúng lớn hơn hoặc bằng 2
Mà a1<a2<a3<a4<a5
Suy ra khoảng cách giũa a1 và a2 và a3 và a4 và a5 nhỏ nhất là 2
Từ a1<a2<a3<a4<a5
Giả sử có hiệu: a1-a5
Mà a1<a5
Nên a1-a5 bé hơn 2 (không thỏa mãn)
Vậy a1<a2<a3<a4<a5 với hiệu hai số bất kì không bé hơn hai không tồn tại









 giúp t với ạ
giúp t với ạ
 giúp mình với ạ
giúp mình với ạ
b: Chọn mp(SAC) có chứa SC
\(I\in SA\subset\left(SAC\right);I\in\left(BIK\right)\)
Do đó: \(I\in\left(SAC\right)\cap\left(BIK\right)\)
Trong mp(ABCD), gọi H là giao điểm của AC và BK
=>\(H\in\left(SAC\right)\cap\left(BIK\right)\)
=>\(\left(SAC\right)\cap\left(BIK\right)=HI\)
Gọi M là giao điểm của HI với SC
=>M là giao điểm của SC với mp(BIK)