

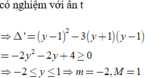
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


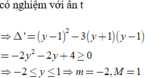

heo me tim gtnn gtln cua bieu thuc:asinx + bcosx (a,b la hang so,a^2+b^2=/o)? | Yahoo Hỏi & Đáp

a) Do \(-1\le sinx\le1,\forall x\in R\).
Nên giá trị lớn nhất của \(y=3-4sinx\) bằng \(3-4.\left(-1\right)=7\)khi \(sinx=-1\)\(\Leftrightarrow x=-\dfrac{\pi}{2}+k\pi\).
Giá trị nhỏ nhất của \(y=3-4sinx\) bằng \(3-4.1=-1\) đạt được khi \(sinx=1\Leftrightarrow x=\dfrac{\pi}{2}+k2\pi\).
b) \(y=2-\sqrt{cosx}\) xác định khi \(0\le cosx\le1\) .
Giá trị lớn nhất của \(y=2-\sqrt{cosx}=2-\sqrt{0}=2\) khi \(cosx=0\Leftrightarrow x=\dfrac{\pi}{2}+k\pi\).
Giá trị nhỏ nhất của \(y=2-\sqrt{cosx}=2-\sqrt{1}=1\) khi \(cosx=1\Leftrightarrow x=k2\pi\).

a) với mọi x thuộc tập xác định của hàm số đã cho ta có
0 ≤ cosx ≤ 1 => y = 2√cosx + 1 ≤ 3.
Giá trị y = 3 đạt được khi cosx = 1 ⇔ x = k2π, k ∈ Z, do đó max y = 3.
b) ta có -1 ≤ sinx ≤ 1, ∀x => 2 ≥ -2sinx ≥ -2 => 1 ≤ y = 3 – 2sinx ≤ 5, ∀x .
Giá trị y = 5 đạt được khi sinx = -1 ⇔ x = −π2+k2π−π2+k2π . k ∈ Z.
Giá trị y = 1 đạt được khi sinx = 1 ⇔ x = π2+k2ππ2+k2π, k ∈ Z.
Vậy max y = 5 ; min y = 1.

\(\Leftrightarrow y\left(sinx+2cosx+3\right)=sinx+cosx\)
\(\Leftrightarrow\left(y-1\right)sinx+\left(2y-1\right)cosx=-3y\)
Theo điều kiện có nghiệm của pt lượng giác bậc nhất:
\(\left(y-1\right)^2+\left(2y-1\right)^2\ge\left(-3y\right)^2\)
\(\Leftrightarrow4y^2+6y-2\le0\)
\(\Rightarrow M+m=\frac{-6}{2.4}=-\frac{3}{4}\)