
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


ta tính
\(y'=3x^2-6x=3x\left(x-2\right)\)
giải pt y'= 0 ta có \(3x\left(x-2\right)=0\) suy ra x=0 hoặc x=2
x y' -3 0 1 2 0 0 y + -55 -1 -3 - -
nhìn vào bảng bt ta có giái trị lớn nhất của hàm số =3 khi x=0, hàm số đạt giá trị nhỏ nhất =-55 khi x=-3
hàm số đạt giái trị lớn nhất =-1 khi x=0, nhỏ nhất =-55 khi x=-3

7/ Em sửa lại đề ạ
Cho hai số thực dương a, b thỏa mãn a+b=4ab
Chứng minh rằng \(\frac{a}{4b^2+1}+\frac{b}{4a^2+1}\ge\frac{1}{2}\)
Đổi biến \(\left(a,b\right)\rightarrow\left(\frac{1}{x},\frac{1}{y}\right)\)
Từ giả thiết => x+y=4
Ta có: BĐT cần CM tương đương với:
\(\frac{\frac{1}{x}}{\frac{4}{y^2}+1}+\frac{\frac{1}{y}}{\frac{4}{x^2}+1}\ge\frac{1}{2}\)\(\Leftrightarrow\frac{y^2}{x\left(4+y^2\right)}+\frac{x^2}{y\left(4+x^2\right)}\ge\frac{1}{2}\left(1\right)\)
Áp dụng BĐT Schwarz, ta có:
∑\(\frac{x^2}{y\left(4+x^2\right)}\ge\frac{\left(x+y\right)^2}{4\left(x+y\right)+xy^2+x^2y}=\frac{16}{16+xy^2+x^2y}\)
Ta chỉ cần chứng minh:
\(xy^2+x^2y\le16\Leftrightarrow xy^2+x^2y\le\frac{1}{4}\left(x+y\right)^3\)
\(\Leftrightarrow xy^2+x^2y\le x^3+y^3\)(luôn đúng)
Do đó (1) đúng. BĐT được chứng minh. Dấu "=" xảy ra khi x=y=2⇔a=b=\(\frac{1}{2}\)
6. (chuyên Hòa Bình)
Cho các số dương x, y, z thỏa mãn: xy+zx+4yz=32
Tìm giá trị nhỏ nhất của\(P=x^2+16y^2+16z^2\)
Áp dụng bất đẳng thức Cauchy cho ba số dương x,y,z ta có
\(\hept{\begin{cases}8y^2+\frac{1}{2}x^2\ge2\sqrt{8y^2.\frac{1}{2}x^2}=4xy\\8z^2+\frac{1}{2}x^2\ge2\sqrt{8z^2.\frac{1}{2}x^2}=4xz\\8y^2+8z^2\ge2\sqrt{8y^2.8z^2}=16yz\end{cases}}\)
Cộng từng vế của ba bđt trên ta có
\(P\ge4\left(xy+xz+4yz\right)=4.32=128\)

ta tính \(y'=\frac{x\left(x-2\right)}{\left(x-1\right)^2}\)
giải pt y'=0
ta có \(x\left(x-2\right)=0\) suy ra x=0 hoặc x=2
bảng bt
x y' y -2 0 1/2 2 0 0 + - -7/3 -1 -3/2
hàm số đạt giá trị lớn nhất =-1 tại x=0, đạt giá trị nhỏ nhất =-7/3 tại x=-2

a, Ta có: \(\left|x-\dfrac{2}{7}\right|\ge0\forall x\)
\(\Rightarrow\left|x-\dfrac{2}{7}\right|+0,5\ge0,5\forall x\)
Hay: \(A\ge0,5\forall x\)
=> Min A = 0,5 tại \(\left|x-\dfrac{2}{7}\right|=0\Rightarrow x=\dfrac{2}{7}\)
b, \(B=\left|x-5\right|+\left|x-2\right|=\left|x-5\right|+\left|2-x\right|\ge\left|x-5+2-x\right|\) =3
=> Min B = 3 tại \(\left(x-5\right)\left(2-x\right)>0\)
=)) Làm nốt
c,Tương tự b
=.= hk tốt!!

a) \(\frac{3}{7}:1=\frac{3}{7}\)
\(\frac{3}{7}:\frac{2}{5}=\frac{3}{7}.\frac{5}{2}=\frac{15}{14}\)
\(\frac{3}{7}:\frac{5}{4}=\frac{3}{7}.\frac{4}{5}=\frac{12}{35}\)
b) + Số chia là 1 =1
+ Số chia là \(\frac{2}{5}\)có tử số =2 bé hơn mẫu số =5 => phân số bé hơn 1
+Số chia là \(\frac{5}{4}\)có tử số = 5 lớn hơn mẫu số = 4 => phân số lớn hơn 1
c) so sánh tương tự câu b nhé bạn.

a) |x-7|=2x+3 (1)
Ta có:|x-7|=x-7<=>x-7 \(\ge\) 0<=>x\(\ge\)7
|x-7|=-(x-7)<=>x-7<0<=>x<7
Nếu x\(\ge\) 7thì (1) <=>x-7=2x+3
<=>x-2x=7+3
<=>-x = 10
<=>x=-10 (ko thỏa mãn đk)
Nếu x<7 thì (1) <=>-(x-7)=2x+3
<=>-x+7=2x+3
<=>-x-2x=-7+3
<=>-3x=-4
<=>x=4/3 (thỏa mãn đk)


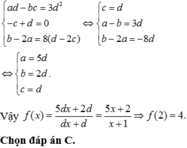
 bit lm bài này k giup tui
bit lm bài này k giup tui
Chọn B.
Phương pháp:
Để tìm GTNN, GTLN của hàm số f trên đoạn [a;b] ta làm như sau:
- So sánh các giá trị vừa tìm được. Số lớn nhất trong các giá trị đó chính là GTLN của f trên [a;b] số nhỏ nhất trong các giá trị đó chính là GTNN của f trên [a;b]