Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

B=|x-2020|+|2021-x|>=|x-2020+2021-x|=1
Dấu = xảy ra khi 2020<=x<=2021

Ta có x = 2020
=> x + 1 = 2021
A = x2021 - 2021x2020 + .... + 2021x - 2021
= x2021 - (x + 1)x2020 + .... + (x + 1)x - (x + 1)
= x2021 - x2021 - x2020 + .... + x2 + x - x + 1
= 1
Vậy A = 1
Ta có : \(x=2020\Rightarrow x+1=2021\)
\(A=x^{2021}-\left(x+1\right)x^{2020}+\left(x+1\right)x^{2019}-\left(x+1\right)x^{2018}+...-\left(x+1\right)x^2+\left(x+1\right)x-2021\)
= x2021 - x2021 - x2020 + x2020 + x2019 - x2019 - x2018 + ... - x3 - x2 + x2 + x - 2021 = x - 2021
mà x = 2020 hay 2020 - 2021 = -1
Vậy với x = 2020 thì A = -1

Ta có : Q(x) = -(x+1)(x+2019) + 2020
= - (x2+2019x+x+2019) + 2020
= -x2 - 2020x - 2019 +2020
= -x2 - 2020x + 1
= - (x2+2020x + 1020100) + 1020101
= - (x+1010)2+1020101
Vì (x+1010)2 \(\ge\) 0 \(\forall x\) nên - (x+1010)2 \(\le0\forall x\)
=> - (x+1010)2+1020101 \(\le\)1020101 với mọi x
=> Q(x) \(\le\)1020101 với mọi x
Ta thấy Q(x) = 1020101 khi (x+1010)2 = 0 => x+1010 = 0 => x = -1010
Vậy Q(x) đạt GTLN là 1020101 khi x = -1010
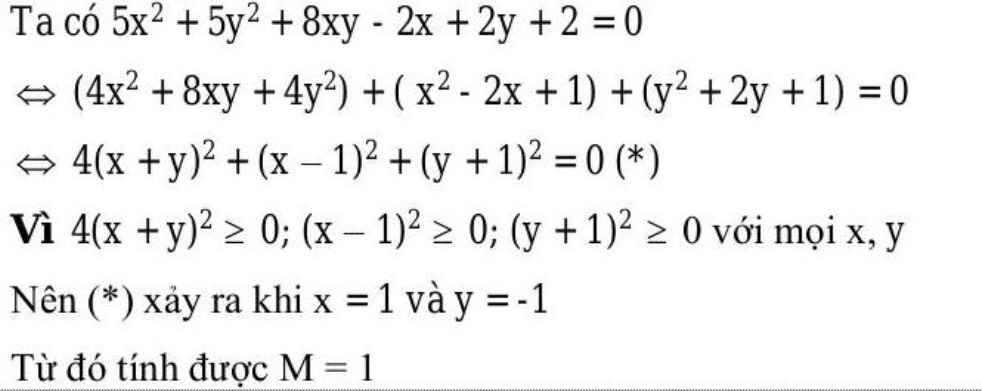
Áp dụng BĐT trị tuyệt đối:
\(M=\left|x-2019\right|+\left|2021-x\right|+2020\left|x-2020\right|\)
\(M\ge\left|x-2019+2021-x\right|+2020\left|x-2020\right|=2+2020\left|x-2020\right|\ge2\)
\(\Rightarrow M_{min}=2\) khi \(\left\{{}\begin{matrix}\left(x-2019\right)\left(2021-x\right)\ge0\\\left|x-2020\right|=0\end{matrix}\right.\) \(\Rightarrow x=2020\)