
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

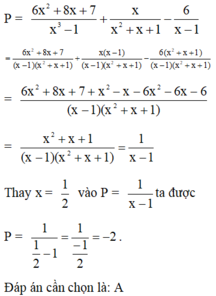

1)
ĐKXĐ: x\(\ne\)3
ta có :
\(\frac{x^2-6x+9}{2x-6}=\frac{\left(x-3\right)^2}{2\left(x-3\right)}=\frac{x-3}{2}\)
để biểu thức A có giá trị = 1
thì :\(\frac{x-3}{2}\)=1
=>x-3 =2
=>x=5(thoả mãn điều kiện xác định)
vậy để biểu thức A có giá trị = 1 thì x=5
1)
\(A=\frac{x^2-6x+9}{2x-6}\)
A xác định
\(\Leftrightarrow2x-6\ne0\)
\(\Leftrightarrow2x\ne6\)
\(\Leftrightarrow x\ne3\)
Để A = 1
\(\Leftrightarrow x^2-6x+9=2x-6\)
\(\Leftrightarrow x^2-6x-2x=-6-9\)
\(\Leftrightarrow x^2-8x=-15\)
\(\Leftrightarrow x=3\) (loại vì không thỏa mãn ĐKXĐ)

\(A=x^2-6x+10=\left(x^2-6x+9\right)+1=\left(x-3\right)^2+1\ge1\forall x\)
Dấu "=" xảy ra <=> x = 3
Vậy MinA = 1
\(B=5x^2-10x+3=5\left(x^2-2x+1\right)-2=5\left(x-1\right)^2-2\ge-2\forall x\)
Dấu "=" xảy ra <=> x = 1
Vậy MinB = -2
\(C=2x^2+8x+y^2-10y+43=2\left(x^2+4x+4\right)+\left(y^2-10y+25\right)+10=2\left(x+2\right)^2+\left(y-5\right)^2+10\ge10\forall x,y\)
Dấu "=" xảy ra <=> x = -2 ; y = 5
Vậy MinC = 10
\(A=x^2-6x+10\)
\(=\left(x^2-6x+9\right)+1\)
\(=\left(x-3\right)^2+1\ge1\forall x\)
Dấu"=" xảy ra khi \(x-3=0\Leftrightarrow x=3\)
Vậy \(Min_A=1\Leftrightarrow x=3\)
b,\(B=5x^2-10x+3\)
\(=5\left(x^2-2x+1\right)-2\)
\(=5\left(x-1\right)^2-2\ge-2\forall x\)
Dấu"=" xảy ra khi \(x-1=0\Leftrightarrow x=1\)
Vậy \(Min_B=-2\Leftrightarrow x=1\)
c,\(C=2x^3+8x+y^2-10+43\)
\(=2x^2+8x+8+y^2-10y+25+10\)
\(=2\left(x^2+4x+4\right)+\left(y^2-10y+25\right)+10\)
\(=2\left(x+2\right)^2+\left(y-5\right)^2+10\ge10\forall x,y\)
Dấu"=" xảy ra khi \(\orbr{\begin{cases}x+2=0\\y-5=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=-2\\y=5\end{cases}}}\)
Vậy \(Min_C=10\Leftrightarrow x=-2;y=5\)

b/ \(3-100x+8x^2=8x^2+x-300\)
\(\Leftrightarrow-101x=-303\)
\(\Rightarrow x=3\)
c/ \(5\left(5x+2\right)-10\left(8x-1\right)=6\left(4x+2\right)-150\)
\(\Leftrightarrow25x+10-80x+10=24x+12-150\)
\(\Leftrightarrow-79x=-158\)
\(\Rightarrow x=2\)
d/ \(3\left(3x+2\right)-\left(3x+1\right)=12x+10\)
\(\Leftrightarrow9x+6-3x-1=12x+10\)
\(\Leftrightarrow-6x=5\)
\(\Rightarrow x=-\frac{5}{6}\)
e/ \(30x-6\left(2x-5\right)+5\left(x+8\right)=210+10\left(x-1\right)\)
\(\Leftrightarrow30x-12x+30+5x+40=210+10x-10\)
\(\Leftrightarrow13x=130\)
\(\Rightarrow x=10\)
\(A=x^2-4x+1=\left(x-2\right)^2-3\ge-3\)
\(\Rightarrow A_{min}=-3\) khi \(x=2\)
\(B=4x^2+4x+11=\left(2x+1\right)^2+10\ge10\)
\(\Rightarrow B_{min}=10\) khi \(x=-\frac{1}{2}\)
\(C=\left(x-1\right)\left(x+6\right)\left(x+2\right)\left(x+3\right)=\left(x^2+5x-6\right)\left(x^2+5x+6\right)\)
\(=\left(x^2+5x\right)^2-36\ge-36\)
\(\Rightarrow C_{min}=-36\) khi \(\left[{}\begin{matrix}x=0\\x=-5\end{matrix}\right.\)
\(D=-x^2-8x-16+21=21-\left(x+4\right)^2\le21\)
\(\Rightarrow C_{max}=21\) khi \(x=-4\)
\(E=-x^2+4x-4+5=5-\left(x-2\right)^2\le5\)
\(\Rightarrow E_{max}=5\) khi \(x=2\)

\(A=\dfrac{6x^2+8x+7+x^2-x-6x^2-6x-6}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=\dfrac{x^2+x+1}{\left(x-1\right)\left(x^2+x+1\right)}=\dfrac{1}{x-1}\)
Để 4A=x-1 thì \(\dfrac{4}{x-1}=x-1\)
=>x-1=2 hoặc x-1=-2
=>x=3(loại) hoặc x=-1(nhận)

Ở các dạng bài này bạn rút gọn đến khi không còn biến x => giá trị biểu thức không đổi
a) (2x+6)(4x^2-12x+36) -8x^3 +5
= 8x^3 -24x^2 + 72x + 24x^2 - 72x - 8x^3 + 5
= 5 ( không đổi)
=> Giá trị của biểu thức không phụ thuộc vào giá trị của biến x
1. (2x + 6 ) (4x2 - 12x + 36)-8x3 + 5
= 8x3 - 24x2 + 72x + 24x2 - 72x - 8x3 + 5
= (8x3 - 8x3) + (-24x2 + 24x2) + (72x - 72x) + 5
= 5
\(\Rightarrow\) Vậy giá trị của biểu thức trên không phụ thuộc vào biến.
2. (x - 1)3 - (x - 3) (x2 + 3x + 9) - 3x (1 - x )
= (x - 1)3- (x - 3) (x2+ x . 3 + 32) - 3x + 3x2
= x3 - 3x2 .1 +3x.12 -13 - x3 - 33 - 3x + 3x2
= (x3-x3) + (-3x2 + 3x2) + (3x - 3x) + (-13 - 33)
= -28
Vậy giá trị của biểu thức trên không phụ thuộng vào biến.
3. (2x - 3) (3x2 + 1) - 6x (x2 - x + 1 ) + 3x2 + 4x
= 6x3 + 2x -9x2 - 3 - 6x3 + 6x2 - 6x + 3x2 + 4x
= (6x3- 6x3) + (-9x2 + 6x2 + 3x2) + (2x - 6x + 4x) -3
= -3
Vậy giá trị của biểu thức trên không phụ thuộc vào biến

\(1,a,A=x^2-6x+25\)
\(=x^2-2.x.3+9-9+25\)
\(=\left(x-3\right)^2+16\)
Ta có :
\(\left(x-3\right)^2\ge0\)Với mọi x
\(\Rightarrow\left(x-3\right)^2+16\ge16\)
Hay \(A\ge16\)
\(\Rightarrow A_{min}=16\)
\(\Leftrightarrow x=3\)