Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ai fan mtp kết bạn nha
ai xem luật nhân quả thì kết bạn nha
chơi truy kích kết bạn nha

a,: ˆMAI+ˆMEI=180oMAI^+MEI^=180o => tứ giác AMEIAMEI nội tiếp
b, tương tự tứ giác EIBNEIBN nội tiếp =>ˆENI=ˆEIB(=12sdEI)ENI^=EIB^(=12sdEI);
ˆEIN=ˆEBN=12sđEB(1)EIN^=EBN^=12sđEB(1)
tứ guacs AMEIAMEI nội tiếp => ˆMIE=ˆMAE=12sđEA(2)MIE^=MAE^=12sđEA(2)
Từ (1) và (2) =>ˆMIN=12sđAB=90o=>MIN^=12sđAB=90o
c, ΔAMI ΔBIN(.....)ΔAMI ΔBIN(.....)
=>AMBI=AIBN=>=>AMBI=AIBN=> đpcm

uầy hello người AE bản sao : bài này :
1. Xét tứ giác CEHD ta có:
góc CEH = 900 (Vì BE là đường cao)
góc CDH = 900 (Vì AD là đường cao)
=> góc CEH + góc CDH = 1800
Mà góc CEH và góc CDH là hai góc đối của tứ giác CEHD. Do đó CEHD là tứ giác nội tiếp
2. Theo giả thiết: BE là đường cao => BE ┴ AC => góc BEA = 900.
AD là đường cao => AD ┴ BC => BDA = 900.
Như vậy E và D cùng nhìn AB dưới một góc 900 => E và D cùng nằm trên đường tròn đường kính AB.
Vậy bốn điểm A, E, D, B cùng nằm trên một đường tròn.
TL
Bn tham khảo
1. Xét tứ giác CEHD ta có:
góc CEH = 900 (Vì BE là đường cao)
góc CDH = 900 (Vì AD là đường cao)
=> góc CEH + góc CDH = 1800
Mà góc CEH và góc CDH là hai góc đối của tứ giác CEHD. Do đó CEHD là tứ giác nội tiếp
2. Theo giả thiết: BE là đường cao => BE ┴ AC => góc BEA = 900.
AD là đường cao => AD ┴ BC => BDA = 900.
Như vậy E và D cùng nhìn AB dưới một góc 900 => E và D cùng nằm trên đường tròn đường kính AB.
Vậy bốn điểm A, E, D, B cùng nằm trên một đường tròn.
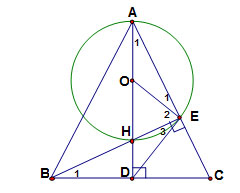
3. Theo giả thiết tam giác ABC cân tại A có AD là đường cao nên cũng là đường trung tuyến
=> D là trung điểm của BC. Theo trên ta có góc BEC = 900.
Vậy tam giác BEC vuông tại E có ED là trung tuyến => DE = 1/2 BC.
4. Vì O là tâm đường tròn ngoại tiếp tam giác AHE nên O là trung điểm của AH => OA = OE => tam giác AOE cân tại O => góc E1 = góc A1 (1).
Theo trên DE = 1/2 BC => tam giác DBE cân tại D => góc E3 = góc B1 (2)
Mà góc B1 = góc A1 (vì cùng phụ với góc ACB) => góc E1 = góc E3 => góc E1 + góc E2 = góc E2 + góc E3
Mà góc E1 + góc E2 = góc BEA = 900 => góc E2 + góc E3 = 900 = góc OED => DE ┴ OE tại E.
Vậy DE là tiếp tuyến của đường tròn (O) tại E.
5. Theo giả thiết AH = 6 Cm => OH = OE = 3 cm.; DH = 2 Cm => OD = 5 cm. Áp dụng định lí Pitago cho tam giác OED vuông tại E ta có ED2 = OD2 – OE2 ↔ ED2 = 52 – 32 ↔ ED=4cm
Hok tốt
Để chứng minh rằng $M, N, E, P, Q$ là một điểm thẳng, ta cần chứng minh rằng chúng đồng quy, tức là nằm trên cùng một đường thẳng.
Trước hết, ta sẽ chứng minh rằng $F, N, E$ đồng quy.
Từ câu hỏi b, ta biết rằng $QI \cdot EF = NI \cdot PI$. Nhân cả hai vế với $\frac{1}{QI}$, ta được:
$$\frac{EF}{QI} = \frac{NI}{QI} \cdot \frac{PI}{QI}$$
Do đó, ta có thể áp dụng định lí Menelaus cho tam giác $NPQ$ và đường thẳng đi qua $F, N, E$ để suy ra rằng $F, N, E$ đồng quy.
Tiếp theo, ta chứng minh rằng $M, N, F$ đồng quy. Ta có:
$$\widehat{FNM} = \widehat{QNP} = 90^\circ - \widehat{PNQ} = \widehat{PMQ} = \widehat{FQM}$$
Do đó, ta có thể áp dụng định lí Euclid đối với tam giác $FNM$ để suy ra rằng $M, N, F$ đồng quy.
Cuối cùng, ta chứng minh rằng $M, N, E$ đồng quy. Ta có:
$$\widehat{FNE} = \widehat{PNQ} = \widehat{PMQ} = \widehat{FNQ}$$
Do đó, ta có thể áp dụng định lí Euclid đối với tam giác $FNE$ để suy ra rằng $M, N, E$ đồng quy.
Vì $F, N, E$ và $M, N, F$ đồng quy, nên ta có $M, N, E, P, Q$ đồng quy. Do đó, chúng nằm trên cùng một đường thẳng, tức là $M, N, E, P, Q$ là một điểm thẳng.
Đúng vậy, ta có $NMP = MQP = QPN = PNM = 90^\circ$. Khi đó, ta có thể suy ra được:
$\angle QNP = \angle QNM + \angle MNP = 90^\circ + 90^\circ = 180^\circ$.$\angle QEP = 90^\circ - \angle EQN = 90^\circ - \angle MQN = \angle QMN$.$\angle EPQ = \angle MPQ - \angle MPE = 90^\circ - \angle QPN - (90^\circ - \angle QNM) = \angle QNM$.Vậy ta có thể kết luận rằng $M, N, E, P, Q$ đồng thời nằm trên đường thẳng do $N$ và $Q$ tạo thành. Do đó, chúng ta có thể chứng minh được $M, N, E, P, Q$ là một điểm thẳng.