Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

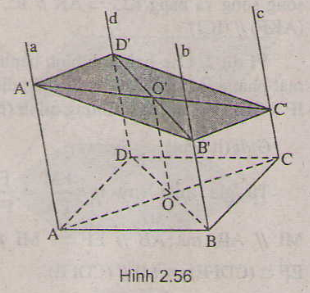
a) Gọi O = AC ∩ BD; O' là trung điểm A'C' thì OO' // AA'
=> OO'// d // b mà O BD
mp (b;d)
=> OO' mp(b;d). Trong mp (b;d) ( mặt phẳng xác định bởi hai đường thẳng song song); d ∩ B'O' = D' là điểm cần tìm
b) Chứng minh mp(a;d) // mp( b;c) , mặt phẳng thứ 3 (A'B'C'D') cắt hai mặt phẳng trên theo hai giao tuyến song song : A'D' // B'C'. Chứng minh tương tự được A'B' // D'C'. Từ đó suy ra A'B'C'D' là hình bình hành

a) Sai
Sửa lại: "Đường thẳng Δ là đường thẳng vuông góc chung của hai đường thẳng chéo nhau a và b nếu Δ cắt cả a và b, đồng thời Δ ⊥ a và Δ ⊥ b"
b) Đúng
c) Đúng
d) Sai
Sửa lại: Đường thẳng đi qua M trên a và vuông góc với a, đồng thời cắt b tại N và vuông góc với b thì đó là đường vuông góc chung của a và b.
e) Sai.

Đáp án C
2. Nếu 3 mặt phẳng đôi một cắt nhau theo 3 giao tuyến phân biệt thì 3 giao tuyến ấy hoặc đồng quy, hoặc đôi một song song với nhau
8. Cho 2 đường thẳng chéo nhau. Có duy nhất một mặt phẳng chứa đường thẳng này và song song với đường thẳng kia
Đáp án D