Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

5 x − y + x + 2 y = 2 2 x + 3 y y + 1 2 . x − 1 2 = x y + 1 2
⇔ 2 x = 5 y x y + x − y − 1 2 = x y + 1 2 ⇔ 2 x = 5 y x y + x − y − 1 = x y + 1 x y + x − y − 1 = − x y − 1 ⇔ 2 x = 5 y x − y = 2 2 x y + x − y = 0
Ta có x − y = 2 .
Chọn đáp án B.

Chọn B.
+ Ta có các số 5x - y; 2x + 3y; x + 2y lập thành CSC nên suy ra
2( 2x + 3y) = 5x – y + x+ 2y hay 2x = 5y (1)
Các số (y + 1)2, xy + 1, (x – 1)2 lập thành CSN suy ra (xy + 1)2 = (y + 1)2(x – 1)2 ⇔ (4 + 2y – 2x)(4xy + 2x – 2y) = 0 (2)
Thay (1) vào (2) ta được: (4 + 2y – 5y)(10y2 + 5y – 2y) = 0
⇔ y(4 – 3y)(10y + 3) = 0 ⇔ y = 0, y = 4/3, y = -3/10.
Vậy 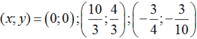

Giả sử 4 nghiệm phân biệt của phương trình là : \(x_1;x_2;x_3;x_4\)
Đặt \(x^2=y\ge0\), ta có phương trình :
\(\Leftrightarrow y^2-\left(3m+5\right)y+\left(m+1\right)^2=0\left(1\right)\)
Ta phải tìm m sao cho (1) có hai nghiệm phân biệt \(0 < y1 < y2\)
Khi đó (1) có 4 nghiệm là : \(x_1=-\sqrt{y_2};x_2=-\sqrt{y_1};x_3=-\sqrt{y_1};x_4=-\sqrt{y_2}\)
Rõ ràng \(x2 < x2 < x3 < x4\)
Theo đầu bài thì bốn nghiệm lập thành cấp số cộng, nên :
\(\Rightarrow x_3+x_1=2x_2\) V \(x_4+x_1=2x_3\)
\(\Leftrightarrow\sqrt{y_1}-\sqrt{y_2}=2\sqrt{y_1}\)
\(\Rightarrow3\sqrt{y_1}=\sqrt{y_2}\)
\(\Leftrightarrow9y_1=y_2\) (*)
Áp dụng Viet cho phương trình (1) ta có hệ :
\(\begin{cases}\Delta=\left(3m+5\right)^2-4\left(m+1\right)^2>0\\S=y_1+y_2=10y_1=3m+5\\P=y_1y_2=9y_1^2=\left(m+1\right)^2\end{cases}\)
\(\Leftrightarrow\begin{cases}m=5\\m=-\frac{25}{19}\end{cases}\)

Chọn A
+ Ba số x + 6 y ,5 x + 2 y ,8 x + y lập thành cấp số cộng nên
x + 6 y + 8 x + y = 2 5 x + 2 y ⇔ 9 x + 7 y = 10 x + 4 y ⇔ x = 3 y
+ Ba số x + 5 3 , y − 1,2 x − 3 y lập thành cấp số nhân nên x + 5 3 2 x − 3 y = y − 1 2 .
Thay x= 3y vào ta được :
3 y + 5 3 2.3 y − 3 y = y − 1 2 ⇔ 3 y + 5 3 .3 y = y 2 − 2 y + 1 ⇔ 9 y 2 + 5 y − y 2 + 2 y − 1 = 0
⇔ 8 y 2 + 7 y − 1 = 0 ⇔ y = − 1 hoặc y = 1 8 .
Với y= -1 thì x= - 3; với y = 1 8 thì x = 3 8 .

Ta có hệ phương trình:
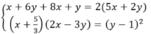
Từ đó ta suy ra
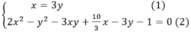
Thế (1) vào (2) ta được: 8y2+7y-1=0⇒y=-1 hoặc y=1/8
Do y < 0 , ta được y = -1, x = -3
Đáp án B

Bài làm
a)dãy số U: \(2,7,12,...x\)
U là cấp số cộng\(\Rightarrow\left\{{}\begin{matrix}d=u_2-u_1=7-2=5\\u_1=2\end{matrix}\right.\)
\(U_n=U_1+\left(n-1\right)d\)
=> \(n=\dfrac{U_n-U_1}{d}+1=\dfrac{x-2}{5}+1=\dfrac{\left(x+3\right)}{5}\)
\(S_n=\dfrac{n\left(U_1+U_n\right)}{2}=\dfrac{\dfrac{\left(x+3\right)}{5}\left(2+x\right)}{2}=\dfrac{\left(x+3\right)\left(x+2\right)}{2.5}=245\)
\(x^2+5x+6=2450\)
\(x^2+5x-2444=0\)
\(\Delta=5^2-4.\left(-2444\right)=9801=\)99^2
\(\left\{{}\begin{matrix}x_1=\dfrac{-5-99}{2}< 0\left(loai\right)\\x_2=\dfrac{-5+99}{2}=47\end{matrix}\right.\)
Đáp số: x=47
b) Xét cấp số cộng 1, 6, 11, ..., 96. Ta có :
\(96=1+\left(n-1\right)5\Rightarrow n=20\)
Suy ra :
\(S_{20}=1+6+11+...+96=\dfrac{20\left(1+96\right)}{2}=970\)
và \(2x.20+970=1010\)
Từ đó : \(x=1\)


Theo giả thiết ta có : \(\begin{cases}\left(5x-y\right)+\left(x+2y\right)=2\left(2x+3y\right)\\\left(y+1\right)^2\left(x-1\right)^2=\left(xy+1\right)^2\end{cases}\)
\(\Leftrightarrow\begin{cases}2x=5y\\x+y=2\end{cases}\) hoặc \(\Leftrightarrow\begin{cases}2x=5y\\xy+x+y=0\end{cases}\)
\(\Leftrightarrow\begin{cases}2x=5y\\x+y=2\end{cases}\) hoặc \(\Leftrightarrow\begin{cases}2x=5y\\y\left(5y\right)+5y+2y=0\end{cases}\)
\(\Leftrightarrow\begin{cases}x=\frac{10}{3}\\y=\frac{4}{3}\end{cases}\) hoặc \(\begin{cases}x=0,y=0\\x=-\frac{3}{4},y=-\frac{3}{10}\end{cases}\)