Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
\(m\ne-1\) ; \(\Delta'=\left(m-3\right)^2-9\left(m+1\right)=m^2-15m\)
a/ Để pt có 2 nghiệm dương pb
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta'>0\\x_1+x_2>0\\x_1x_2>0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m^2-15m>0\\\frac{2\left(m-3\right)}{m+1}>0\\\frac{9}{m+1}>0\end{matrix}\right.\) \(m>15\)
b/ Để pt có 2 nghiệm pb thỏa \(x_1< -1< x_2\)
\(\Leftrightarrow f\left(-1\right)< 0\)
\(\Leftrightarrow\left(m+1\right).1+2\left(m-3\right)+9< 0\)
\(\Leftrightarrow3m+4< 0\Rightarrow m< -\frac{4}{3}\)
c/ Để pt có 2 nghiệm pb thỏa \(x_1< x_2< 2\)
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta'>0\\\left(x_1-2\right)\left(x_2-2\right)>0\\\frac{x_1+x_2}{2}< 2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m^2-15m>0\\x_1x_2-2\left(x_1+x_2\right)+4>0\\x_1+x_2< 4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m^2-15m>0\\\frac{9}{m+1}+\frac{4\left(m-3\right)}{m+1}+4>0\\\frac{2\left(m-3\right)}{m+1}-4< 0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m^2-15m>0\\\frac{8m+1}{m+1}>0\\\frac{-2\left(m+5\right)}{m+1}< 0\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}m< -5\\-1< m< -\frac{1}{8}\\m>15\end{matrix}\right.\)
Bạn tự soát lại tính toán nhé
Bài 2:
a: \(\text{Δ}=\left(4m+2\right)^2-4\left(4m+3\right)\)
\(=16m^2+16m+4-16m-12=16m^2-8\)
Để phương trình có hai nghiệm thì \(2m^2>=1\)
=>\(\left[{}\begin{matrix}m>=\dfrac{1}{\sqrt{2}}\\m< =-\dfrac{1}{\sqrt{2}}\end{matrix}\right.\)
c: \(A=\left(x_1+x_2\right)^3-3x_1x_2\left(x_1+x_2\right)\)
\(=\left(4m+2\right)^3-3\cdot\left(4m+3\right)\left(4m+2\right)\)
\(=64m^3+96m^2+48m+8-3\left(16m^2+20m+6\right)\)
\(=64m^3+96m^2+48m+8-48m^2-60m-18\)
\(=64m^3+48m^2-12m-10\)
1,
a, với m=1 , phương trình có nghiệm x=\(\frac{1}{2}\)
với m\(\ne1\) , \(_{\Delta}\)=m
- nếu m< 0 : pt vô nghiệm
-nếu m=0: pt có 1 nghiệm kép x=1
-nếu m>0( và m\(\ne\)1) : pt có 2 nghiệm
\(x_1=\frac{-1-\sqrt{m}}{m-1}\) và \(x_2=\frac{-1+\sqrt{m}}{m-1}\)
b, pt có 2 nghiệm trái dấu nếu
m-1\(\ne\)0 và \(\frac{-1}{m-1}\)<0 \(\Leftrightarrow\)m>1
c, \(m\ne1\) và m>0, pt có 2 nghiệm x1 và x2
1=x12 +x22=(x1+x2)2-2x1x2=\(\left(\frac{2}{m-1}\right)^2+\frac{2}{m-1}\Rightarrow m=2+\sqrt{5}\)
2,
giả sử 2 pt đều có nghiệm thì phải có:
\(\Delta_1=1-4a\ge0\) và \(\Delta_2=a^2-4\ge0\Leftrightarrow a\le-2\)
giả sử k là 1 nghiệm chung thì ta phải có:
k2+k+a=k2+ka+1
\(\Rightarrow\) k(a-1)=a-1 \(\Rightarrow\)k=1 (vì \(a\le-2\) nên a-1\(\ne\)0)
thay k=1 vào 1 pt ta tính được a=-2
thử lại: a=-2 vào các pt ta thấy dúng là 2 pt có nghiệm chung là x=1
Bài 3:
a: Để pt có hai nghiệm trái dấu thì m+5<0
=>m<-5
b: \(\text{Δ}=\left(m+2\right)^2-4\left(m+5\right)\)
\(=m^2+4m+4-4m-20=m^2-16\)
Để phương trình có hai nghiệm phân biệt thì m^2-16>0
=>m>4 hoặc m<-4
c: x1^2+x2^2=23
=>(x1+x2)^2-2x1x2=23
=>(m+2)^2-2(m+5)=23
=>m^2+4m+4-2m-10-23=0
=>m^2+2m-29=0
hay \(m=-1\pm\sqrt{30}\)
d: Để pt có hai nghiệm âm phân biệt thì
\(\left\{{}\begin{matrix}m\in R\backslash\left[-4;4\right]\\m+2< 0\\m+5>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m\in R\backslash\left[-4;4\right]\\-5< m< -2\end{matrix}\right.\Leftrightarrow m\in[-4;-2)\)
a) Xét: x2 - 4mx + 9.(m – 1)2 = 0 (1)
Δ’ = (2.m)2 – 9.(m – 1)2 = 4m2 – 9.(m2 – 2m + 1) = -5m2 + 18m – 9
Phương trình (1) có nghiệm ⇔ Δ’ ≥ 0
⇔ -5m2 + 18m – 9 ≥ 0
⇔ 5m2 - 18m + 9 ≤ 0
⇔ (5m – 3)(m – 3) ≤ 0
⇔ 3/5 ≤ m ≤ 3.
b) + x1 ; x2 là hai nghiệm của (1) nên theo định lý Vi-et ta có:
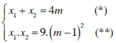
+ Tìm hệ thức giữa x1 và x2 không phụ thuộc vào m.
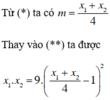
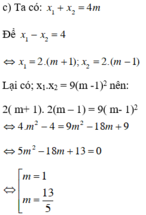
Thử lại:
+ m = 1, (1) trở thành x2 – 4x = 0 có hai nghiệm x = 0; x = 4 có hiệu bằng 4
+ m = 13/5, (1) trở thành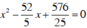 
có hai nghiệm x = 7,2 và x = 3,2 có hiệu bằng 4.
Vậy m = 1 hoặc m = 13/5.
Akai HarumaAce LegonaNguyễn Thanh HằngNguyễn Huy TúMysterious PersonVõ Đông Anh TuấnNguyễn Thanh HằngVũ Minh Tuấn
\(\Leftrightarrow\left(x+1\right)\left(x+2\right)\left(x+4\right)\left(x+5\right)-m-1=0\)
\(\Leftrightarrow\left(x^2+6x+5\right)\left(x^2+6x+8\right)-m-1=0\)
Đặt \(x^2+6x+7=\left(x+3\right)^2-2=t\ge-2\) ta được:
\(\left(t-2\right)\left(t+1\right)-m-1=0\)
\(\Leftrightarrow t^2-t-m-3=0\) (1)
a/ Bạn tự giải (thay số bấm máy ez)
b/ Pt có nghiệm thỏa \(x^2+6x+7\le0\) khi và chỉ khi (1) có nghiệm \(t\in\left[-2;0\right]\)
Ta có: \(\left(1\right)\Leftrightarrow t^2-t-3=m\)
Xét hàm \(f\left(t\right)=t^2-t-3\) trên \(\left[-2;0\right]\)
\(a=1>0;\) \(-\frac{b}{2a}=\frac{1}{2}>0\Rightarrow f\left(t\right)\) nghịch biến trên \(\left[-2;0\right]\)
\(\Rightarrow f\left(0\right)\le f\left(t\right)\le f\left(-2\right)\Rightarrow-3\le f\left(t\right)\le3\)
\(\Rightarrow-3\le m\le3\)
Giả sử pt có 2 nghiệm và \(x_1\) là nghiệm lớn hơn
\(x_1+x_2=\frac{a+b}{ab}\)
\(x_1-x_2=\sqrt{\left(x_1-x_2\right)^2}=\sqrt{\left(x_1+x_2\right)^2-4x_1x_2}=\sqrt{\frac{\left(a+b\right)^2}{a^2b^2}-\frac{4}{ab}}\)
\(=\sqrt{\frac{a^2+2ab+b^2-4ab}{a^2b^2}}=\sqrt{\frac{\left(a-b\right)^2}{a^2b^2}}=\frac{a-b}{ab}\)
\(\Rightarrow\frac{x_1+x_2}{x_1-x_2}=\frac{a+b}{a-b}\)