Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.
Ta có: T = A(1 + r) n trong đó n là số kỳ hạn, r là lãi suất theo kỳ hạn
TH1: r = 1%/tháng và n = 12 khi đó T1 = A(1 + 0,01)12
TH2: r = 3%/tháng và n = 4 khi đó T2 = A(1 + 0,03)4
TH3: r = 6%/tháng và n = 2 khi đó T3 = A(1 + 0,06)2
TH4: r = 12%/tháng và n = 1 khi đó T4 = A(1 + 0,12)
Từ 4 kết quả trên bạn A nên chọn phương án gửi theo kỳ hạn 1 tháng để có số tiền là lớn nhất.

Đáp án C.
Giả sử bác An gửi số tiền tối thiểu hàng tháng là T (đồng). Đặt r = 0,45%.
Hết tháng thứ nhất bác An nhận được số tiền cả gốc và lãi là
T 1 = T + T . r = T . 1 + r .
Hết tháng thứ hai bác An nhận được số tiền cả gốc và lãi là
T 2 = T . 2 + r + T . 2 + r . r = T . r + 1 2 + r + 1 .
Bằng phương pháp quy nạp toán học, ta chứng minh được rằng sau n tháng gửi tiết kiệm thì bác An nhận được số tiền cả gốc và lãi là
T n = T 1 + r n + 1 + r n − 1 + ... + 1 + r .
Dễ dàng tính được T n = T r . 1 + r . 1 + r n − 1 .
Suy ra số tiền lãi sau n tháng gửi tiết kiệm là
L n = T n − T n = T r . 1 + r . 1 + r n − 1 − T n .
Theo giả thiết, ta có n = 36 , L 36 ≥ 30 000 000. Suy ra T ≥ 9 493 000.
Phân tích phương án nhiễu.
Phương án A: Sai do HS tính chỉ gửi 35 tháng.
Phương án B: Sai do HS sử dụng công thức của bài toán tính lãi kép và hiểu đề bài yêu cầu số tiền thu được sau 3 năm đủ để mua xe máy có trị giá 30 triệu đồng nên tìm được T = 25 523 000.
Phương án C: Sai do HS giải đúng như trên nhưng lại làm tròn T = 9 492 000.

Chọn C
Gọi P là số tiền ông A gửi lúc đầu. Để rút được 100 triệu đồng sau 5 năm ta phải có
P ( 1 + 0 , 068 ) 5 = 100000000
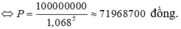
Vì số tiền gửi là tròn triệu đồng nên ông A phải gửi tối thiểu 72 triệu đồng.
Chọn C
Gọi P là số tiền ông A gửi lúc đầu. Để rút được 100 triệu đồng sau 5 năm ta phải có
P ( 1 + 0 , 068 ) 5 = 100000000
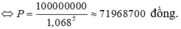
Vì số tiền gửi là tròn triệu đồng nên ông A phải gửi tối thiểu 72 triệu đồng.

Lời giải:
Đổi 2 năm là 24 tháng. Lãi suất 6%/năm tương ứng với $0,5$ %/tháng
Giả sử phải gửi $x$ (triệu đồng)
Ta có: $x(1+\frac{0,5}{100})^{24}=500$
$\Rightarrow x=\frac{500}{1,005^{24}}=443,6$ (triệu đồng)
$\Rightarrow x=\frac{500}{1,06^2}=445$ (triệu đồng)