
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi d là UCLN(2n+4;4n+6)
=>2n+4 chia hết cho d và 4n+6 chia hết cho d
=>2.(2n+4)=4n+8 chia hết cho d
=>(4n+8)-(4n+6)=4n+8-4n-6=2 chia hết cho d
=>d là 2 (vì 2n+4 và 4n+6 chia hết cho 2 và 2>1)
Vậy UCLN(2n+4;4n+6)=2

2.(3-6x)+8.(x-5)=-42
2.3-2.6x+8.x-8.5=-42
6-2.6x+8.x-40=-42
2.6x+8.x-40=6-(-42)
2.6x+8.x-40=48
2.6x+8x=48+40
2.6x+8x=88
12x+8x=88
x.(12+8)=88
x20=88
x=88/20
x=4,4

gọi 2 số lẻ liên tiếp là 2k+1 và 2k+3; ƯCLN(2k+1;2k+3)
ta có : 2k+1 chia hết cho d
2k+3 chia hết cho d
-> 2k+3-(2k+1) chia hết cho d
-> 2k+3-2k-1 chia hết cho d
-> 2 chia hết cho d
vậy d thuộc Ư(2)={ 1;2 }
vì 2k+1 và 2k+3 là 2 số lẻ liên tiếp nên d không thể bằng 2
-> d=1
vậy 2k+1;2k+3 là 2 số nguyên tố cùng nhau
vậy 2 số lẻ liên tiếp là 2 số nguyên tố cùng nhau (đpcm)


Ta có :
50 = 52 x 2
Số ước của 50 :
( 2 + 1 ) ( 1 + 1 ) = 6 ( ước )
Ta có :
50 = 52 x 2
Số ước của 50 :
( 2 + 1 ) ( 1 + 1 ) = 6 ( ước )

200 : [ 100 - ( 52. 20100 +50 ) ] + ( 72 - 6. 23 )2021
= 200 : [ 100 - ( 25 . 1 + 50 ) ] + ( 49 - 6 . 8 ) 2021
= 200 : [ 100 - ( 25 + 50 ) ] + ( 49 - 48 ) 2021
= 200 : [ 100 - 75 ] + 12021
= 200 : [ 100 - 75 ] + 1
= 200 : 25 + 1
= 8 + 1
= 9
\(200:[100-\left(5^2.2021^0+50\right)]+\left(7^2-6.2^3\right)^{2021}\)
\(200:[100-\left(25+50\right)]+\left(49-48\right)^{2021}\)
\(200:25+1\)
=8+1=9
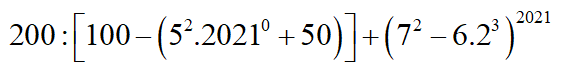
= -15/14 + 15/7 - -1/6 + 8/7
= 5/14 - -1/6 + 8/7
= 11/21 + 8/7
= 5/3
= 5/3