Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C M N Q P O R S T A B C H M D I A B C D K G M K E P F (Hình a) (Hình b) (Hình c) Q I
Bài toán 1: (Hình a)
Gọi đường thẳng qua N vuông góc với AN cắt AC tại R, qua P kẻ đường thẳng song song với BC. Đường thẳng này cắt AM,AN,BC lần lượt tại S,T,K.
Ta thấy \(\Delta\)APR có AN vừa là đường cao, đường phân giác => \(\Delta\)APR cân tại A => AP = AR, NP = NR
Áp dụng hệ quả ĐL Thales \(\frac{BM}{PS}=\frac{CM}{KS}\left(=\frac{AM}{AS}\right)\)=> PS = KS
Áp dụng ĐL đường phân giác trong tam giác: \(\frac{TK}{TP}=\frac{AK}{AP}\Rightarrow\frac{ST+SK}{TP}=\frac{AK}{AR}\)
\(\Rightarrow\frac{2ST+PT}{TP}=\frac{AR+RK}{AR}\Rightarrow\frac{2ST}{TP}=\frac{RK}{AR}\)
Dễ thấy NS là đường trung bình của \(\Delta\)RKP => RK = 2NS. Do đó \(\frac{ST}{TP}=\frac{NS}{AR}\)
Đồng thời NS // AR, suy ra \(\frac{ST}{TP}=\frac{NS}{AR}=\frac{SQ}{QA}\)=> QT // AP (ĐL Thaels đảo)
Mà AP vuông góc PO nên QT vuông góc PO. Từ đây suy ra T là trực tâm của \(\Delta\)POQ
=> QO vuông góc PT. Lại có PT // BC nên QO vuông góc BC (đpcm).
Bài toán 2: (Hình b)
Ta có IB = IC => \(\Delta\)BIC cân tại I => ^IBC = ^ICB = ^ACB/2 => \(\Delta\)MCI ~ \(\Delta\)MBC (g.g)
=> MC2 = MI.MB. Xét \(\Delta\)AHC có ^AHC = 900 , trung tuyến HM => HM = MC
Do đó MH2 = MI.MB => \(\Delta\)MIH ~ \(\Delta\)MHB (c.g.c) => ^MHI = ^MBH = ^MBC = ^MCI
=> Tứ giác CHIM nội tiếp. Mà CI là phân giác ^MCH nên (IH = (IM hay IM = IH (đpcm).
Bài toán 3: (Hình c)
a) Gọi đường thẳng qua C vuông góc CB cắt MK tại F, DE cắt BC tại Q, CG cắt BD tại I.
Áp dụng ĐL Melelaus:\(\frac{MB}{MC}.\frac{GA}{GB}.\frac{DC}{DA}=1\)suy ra \(\frac{DC}{DA}=2\)=> A là trung điểm DC
Khi đó G là trọng tâm của \(\Delta\)BCD. Do CG cắt BD tại I nên I là trung điểm BD
Dễ thấy \(\Delta\)BCD vuông cân tại B => BI = CM (=BC/2). Từ đó \(\Delta\)IBC = \(\Delta\)MCF (g.c.g)
=> CB = CF => \(\Delta\)BCF vuông cân ở C => ^CBA = ^CBF (=450) => B,A,F thẳng hàng
=> CA vuông góc GF. Từ đó K là trực tâm của \(\Delta\)CGF => GK vuông góc CF => GK // CM
Theo bổ đề hình thang thì P,Q lần lượt là trung điểm GK,CM. Kết hợp \(\Delta\)CEM vuông ở E
=> EQ=CM/2. Áp dụng ĐL Melelaus có \(\frac{GD}{GM}.\frac{EQ}{ED}.\frac{CM}{CQ}=1\)=> \(\frac{EQ}{ED}=\frac{1}{4}\)
=> \(\frac{ED}{CM}=2\)=> DE = 2CM = BC (đpcm).
b) Theo câu a thì EQ là trung tuyến của \(\Delta\)CEM vuông tại E => EQ = QC => ^QEC = ^QCE
Vì vậy ^PEG = ^QEC = ^QCE = ^PGE => \(\Delta\)EPG cân tại P => PG = PE (đpcm).

a, xét tg BEM và tg CFM có : ^CFM = ^BEM = 90
^ABC = ^ACCB do tg ABC cân tại A (gt)
CM = BM do M là trung điểm của BC (gt)
=> tg BEM = tg CFM (ch-gn) (1)
b, (1) => CF = BE (đn)
AB = AC do tg ABC cân tại A (gt)
CF + AF = AC
BE + AE = AB
=> AF = AE
Bài giải
A B C M E F G
a, Xét 2 tam giác vuông BME và CMF có :
MB = MC ( AM là đường trung tuyến ) : cạnh huyền
\(\widehat{B}=\widehat{C}\) ( tam giác ABC cân ) : góc nhọn
\(\Rightarrow\text{ }\Delta BME =\Delta CMF ( ch-gn ) \) ( 1 )
b, Từ ( 1 ) => BE = CF ( 2 cạnh tương ứng )
Mà AB = AE + BE
AC = AF + CF
Mà BE = CF => AE = AF
c, Ta có :
\(AG=BG=\frac{2}{3}AM\text{ }\Rightarrow\text{ }\frac{AG+BG}{2}=\frac{\frac{2}{3}AM+\frac{2}{3}AM}{2}=\frac{\frac{4}{3}AM}{2}=\frac{3}{2}AM>BG\)
\(\Rightarrow\text{ }ĐPCM\)

a: Xét ΔABE và ΔADE có
AB=AD
\(\widehat{BAE}=\widehat{DAE}\)
AE chung
DO đó: ΔABE=ΔADE
b: Ta có: ΔABD cân tại A
mà AI là đường phân giác
nên I là trung điểm của BD
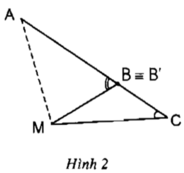



Ta có: góc AB’M là góc ngoài của tam giác MB’C
Nên ∠(BMC) + ∠C= (AB'M) ⇒ ∠(AB'M) > ∠C