Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

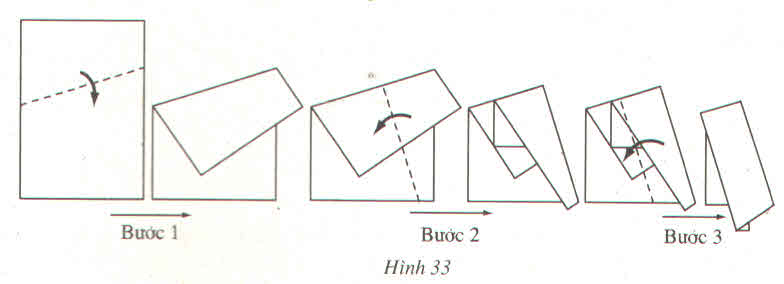
Xem hình và quan sát bước 4
Vậy các nếp gập là hình ảnh của một đường thẳng vuông góc với hai đường thẳng song song .
Xem hình và quan sát khi trải tờ giấy ra ta thấy các nếp gấp là hình ảnh của một đường thẳng vuông góc với hai đường thẳng song song.

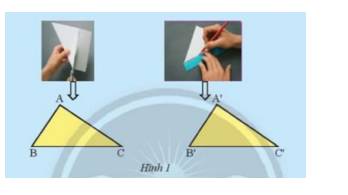
Ta thấy 2 tam giác có các cặp góc bằng nhau \(\widehat A = \widehat {A'}\); \(\widehat B = \widehat {B'}\); \(\widehat C = \widehat {C'}\)
2 tam giác có các cặp cạnh bằng nhau AC = A’C’; AB = A’B’; BC = B’C’

Nếp gấp zt vuông góc với đường thẳng xy tại O. Có bốn góc vuông là xOz,yOz,yOt,tOx.

Quan sát hình vẽ ta thấy:
- Các cạnh tương ứng bằng nhau.
- Các góc tương ứng bằng nhau.

Xét 2 tam giác ABC và MNP có:
AB=MN (gt)
\(\widehat {BAC} = \widehat {NMP}\) (gt)
AC=MP (gt)
Vậy \(\Delta ABC = \Delta MNP\)(c.g.c)

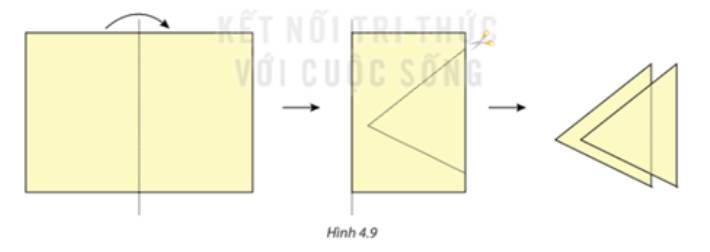


Ta thấy sau khi cắt 2 cạnh của tam giác bằng nhau