K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
LH
0
TD
52
LA
9 tháng 1 2024
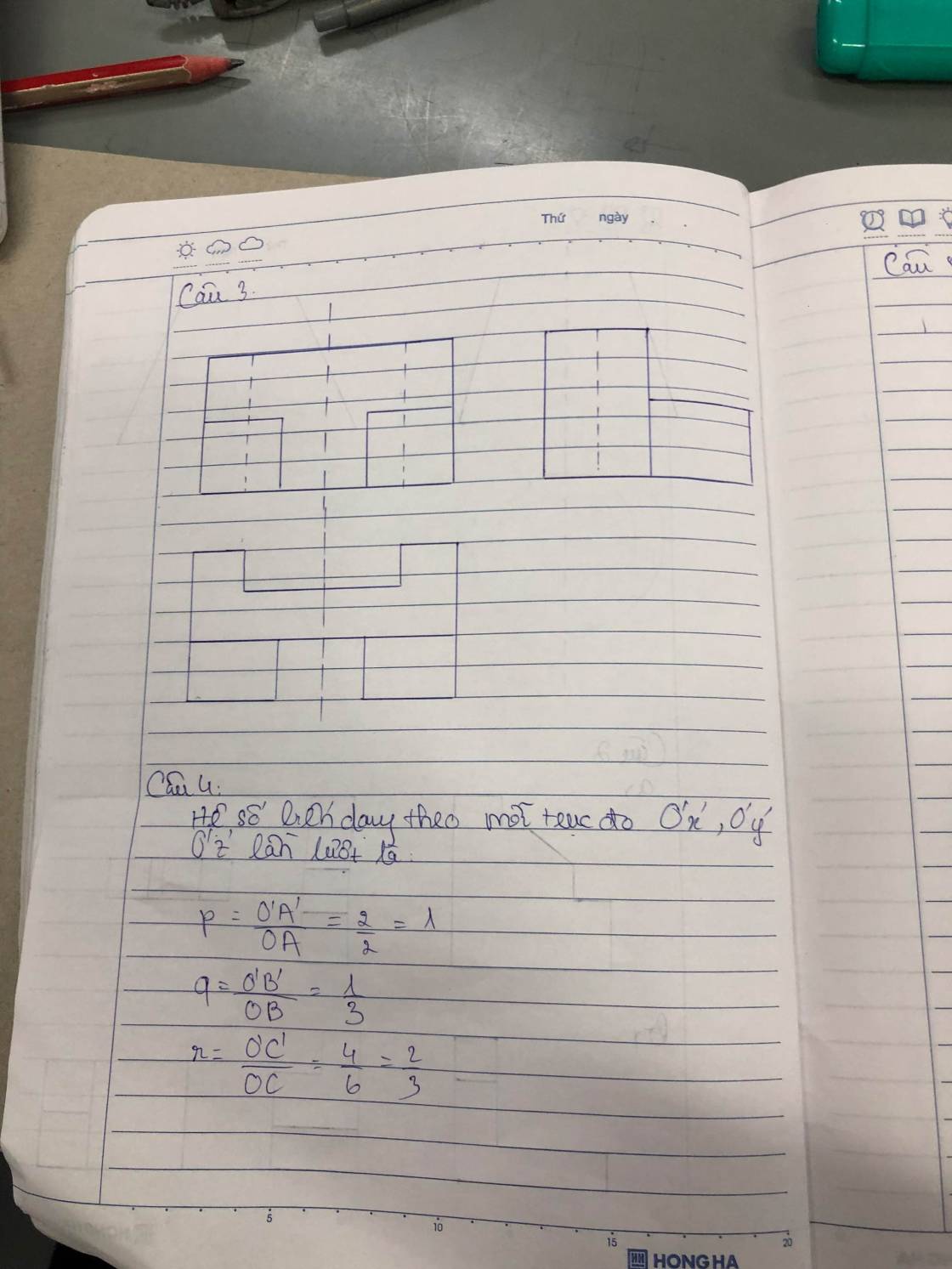
Hệ số biến dạng theo mỗi trục đo O'x', O'y', O'z' lần lượt là:
p=O'A'OA=22=1�=�'�'��=22=1;
q=O'B'OB=13�=�'�'��=13;
r=O'C'OC=46=23�=�'�'��=46=23.
TD
8
CL
18 tháng 9 2019
2 : cho ab=cd(a,b,c,d≠0)ab=cd(a,b,c,d≠0) và đôi 1 khác nhau, khác đôi nhau
Chứng minh :
a) C1: Đặt \(\frac{a}{b}=\frac{c}{d}=k\)\(\Rightarrow\left\{{}\begin{matrix}a=kb\\c=kd\end{matrix}\right.\)
\(\frac{a-b}{a+b}=\frac{kb-b}{kb+b}=\frac{b\left(k-1\right)}{b\left(k+1\right)}=\frac{k-1}{k+1}\)
\(\frac{c-d}{c+d}=\frac{kd-d}{kd+d}=\frac{d\left(k-1\right)}{d\left(k+1\right)}\frac{k-1}{k+1}\)
5 tháng 2 2022
Bài 1:
a: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{2}=\dfrac{y}{\dfrac{3}{2}}=\dfrac{z}{\dfrac{4}{3}}=\dfrac{x-y}{2-\dfrac{3}{2}}=\dfrac{15}{\dfrac{1}{2}}=30\)
Do đó: x=60; y=45; z=40
b: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{10}=\dfrac{y}{15}=\dfrac{z}{21}=\dfrac{x+y+z}{10+15+21}=\dfrac{92}{46}=2\)
Do đó: x=20; y=30; z=42
22 tháng 9 2023
Tham khảo:
Mẫu a, b là mẫu số liệu ghép nhóm.
a)
- Có 5 sinh viên chi dưới 50 nghìn đồng cho việc thanh toán cước điện thoại trong tháng.
- Có 12 sinh viên chi từ 50 đến dưới 100 nghìn đồng cho việc thanh toán cước điện thoại trong tháng.
- Có 23 sinh viên chi từ 100 đến dưới 150 nghìn đồng cho việc thanh toán cước điện thoại trong tháng.
- Có 17 sinh viên chi từ 150 đến dưới 200 nghìn đồng cho việc thanh toán cước điện thoại trong tháng.
- Có 3 sinh viên chi từ 200 đến dưới 250 nghìn đồng cho việc thanh toán cước điện thoại trong tháng.
Như vậy, đa số sinh viên chi từ 100 đến dưới 150 nghìn đồng mỗi tháng cho cước điện thoại và có ít sinh viên chi trên 200 nghìn đồng cho cước điện thoại mỗi tháng.
b)
- Có 7 ngày có nhiệt độ từ đến dưới.
- Có 15 ngày có nhiệt độ từ đến dưới.
- Có 12 ngày có nhiệt độ từ đến dưới.
- Có 6 ngày có nhiệt độ từ đến dưới.
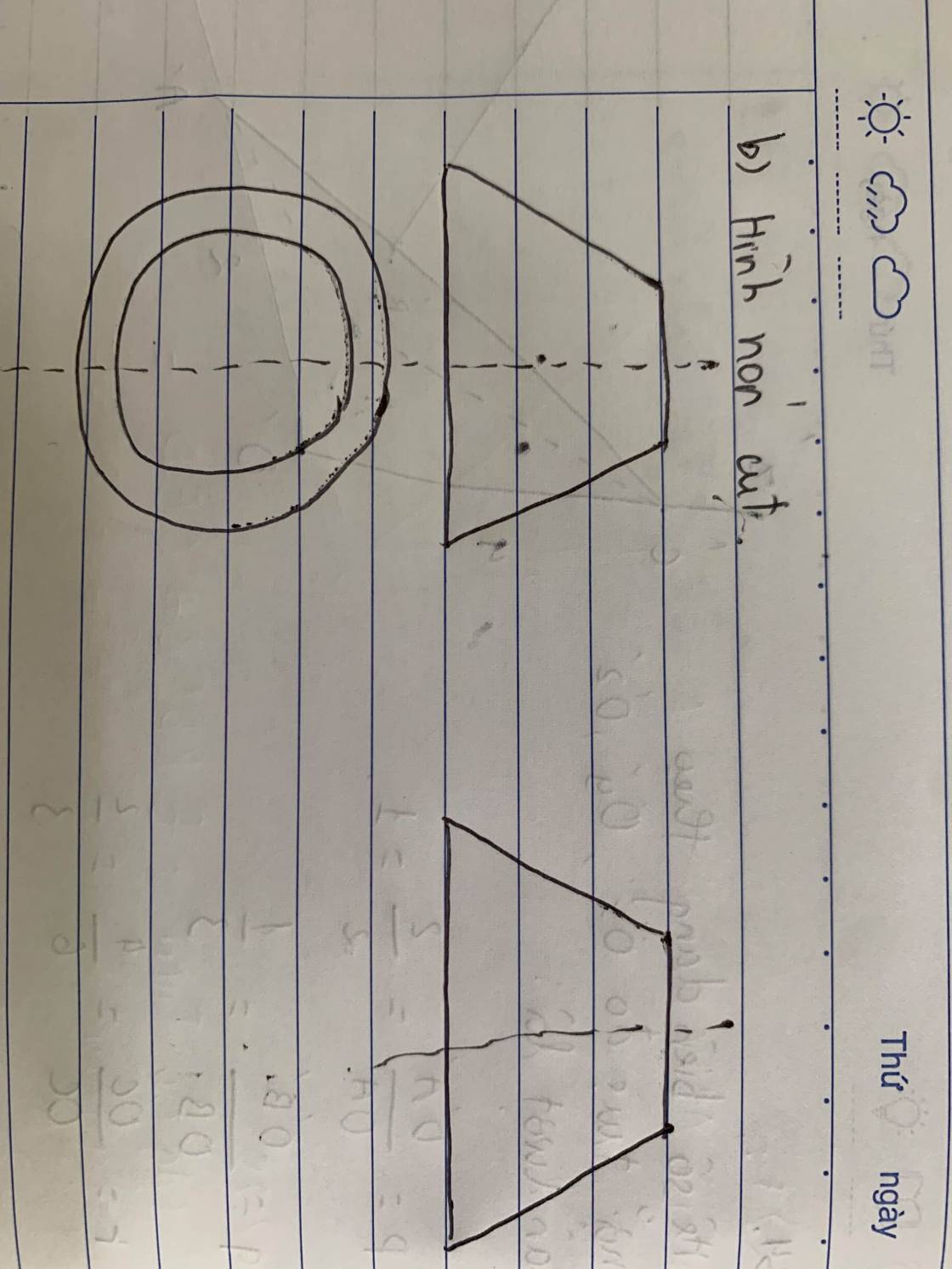
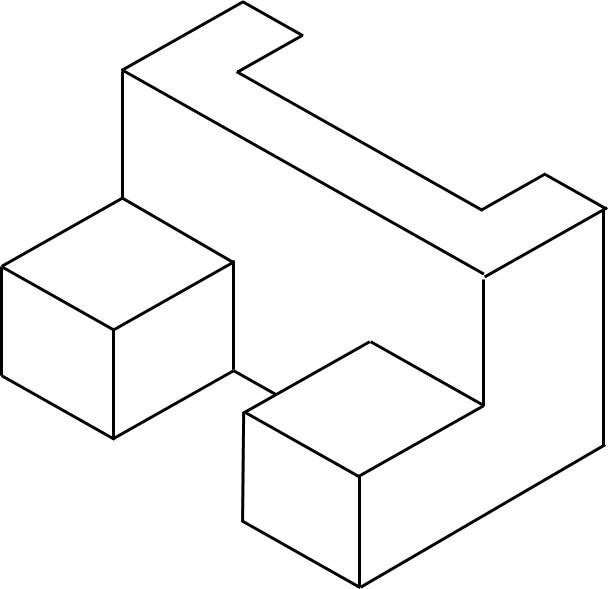
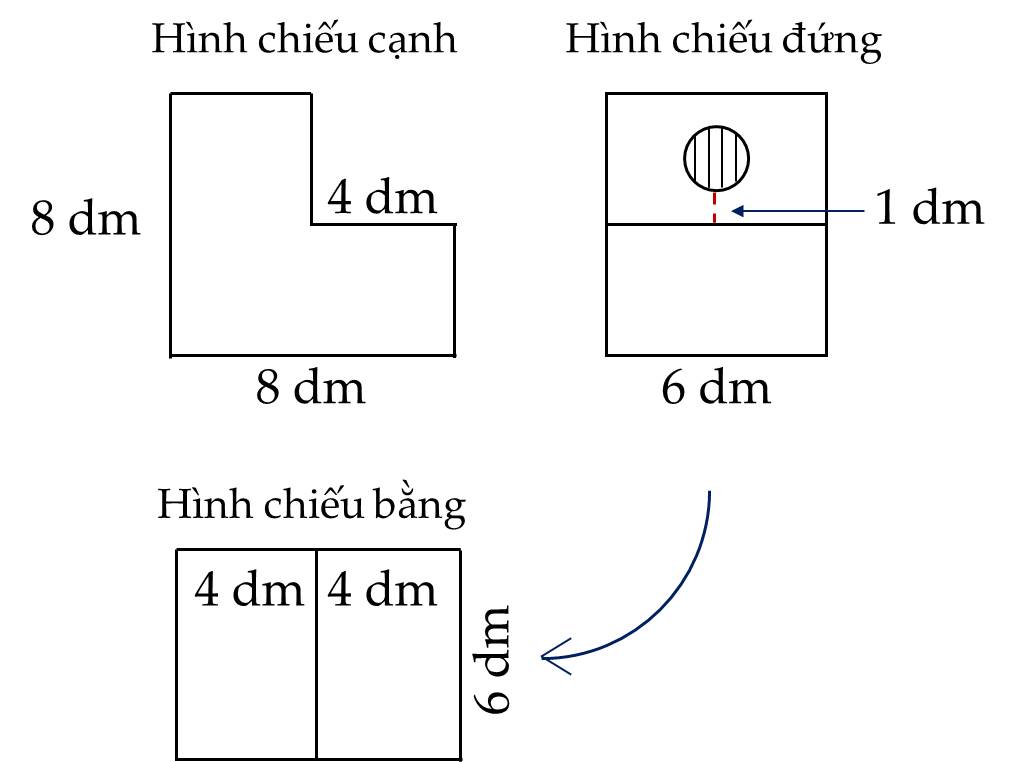
1.
Do \(SB\perp\left(ABC\right)\Rightarrow AB\) là hình chiếu của SA lên (ABC)
\(\Rightarrow\widehat{SAB}\) là góc giữa SA và (ABC)
\(cos\widehat{SAB}=\dfrac{AB}{SA}=\dfrac{\sqrt{2}}{2}\Rightarrow\widehat{SAB}=45^0\)
b.
\(SB\perp\left(ABC\right)\Rightarrow CB\) là hình chiếu của SC lên (ABC)
\(\Rightarrow\widehat{SCB}\) là góc giữa SC và (ABC)
\(SB=\sqrt{SA^2-AB^2}=a\)
\(BC=AB\sqrt{2}=a\sqrt{2}\)
\(tan\widehat{SCB}=\dfrac{SB}{BC}=\dfrac{1}{\sqrt{2}}\Rightarrow\widehat{SCB}=35^016'\)
c.
\(\left\{{}\begin{matrix}SB\perp\left(ABC\right)\\\left(SAB\right)\cap\left(SCB\right)=SB\\\end{matrix}\right.\)
\(\Rightarrow\left[A,SB,C\right]=\widehat{ABC}=45^0\) (góc đáy tam giác vuông cân)
2.
Do \(SA\perp\left(ABCD\right)\Rightarrow\) AB là hình chiếu của SB lên (ABCD)
\(\Rightarrow\widehat{SBA}\) là góc giữa SB và (ABCD)
\(tan\widehat{SBA}=\dfrac{SA}{AB}=\sqrt{3}\Rightarrow\widehat{SBA}=60^0\)
b.
Do \(SA\perp\left(ABCD\right)\Rightarrow AD\) là hình chiếu của SD lên (ABCD)
\(\Rightarrow\widehat{SDA}\) là góc giữa SD và (ABCD)
\(tan\widehat{SDA}=\dfrac{SA}{AD}=\dfrac{SA}{BC}=\dfrac{\sqrt{6}}{2}\Rightarrow\widehat{SDA}\approx50^046'\)
c.
\(SA\perp\left(ABCD\right)\Rightarrow AC\) là hình chiếu của SC lên (ABCD)
\(\Rightarrow\widehat{SCA}\) là góc giữa SC và (ABCD)
\(SC=\sqrt{AB^2+BC^2}=a\sqrt{3}\)
\(tan\widehat{SCA}=\dfrac{SA}{AC}=1\Rightarrow\widehat{SCA}=45^0\)
d.
\(\left\{{}\begin{matrix}\left(SAD\right)\cap\left(SAB\right)=SA\\AD\perp SA\\AB\perp SA\end{matrix}\right.\) \(\Rightarrow\left[D,SA,B\right]=\widehat{DAB}=90^0\)
e.
\(\left\{{}\begin{matrix}\left(SAC\right)\cap\left(SAB\right)=SA\\AC\perp SA\\AB\perp SA\end{matrix}\right.\) \(\Rightarrow\left[B,SA,C\right]=\widehat{BAC}\)
\(cos\widehat{BAC}=\dfrac{AB}{AC}=\dfrac{1}{\sqrt{3}}\Rightarrow\widehat{BAC}\approx54^044'\)