Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. Điểm biểu diễn các số: - 2; - 3; - 1 đều đặt ở bên trái điểm 0 nên các số này đều nhỏ hơn số 0;
Điểm biểu diễn các số 1; 2; 4 đều đặt ở bên phải điểm 0 nên các số này đều lớn hơn số 0.
b. Điểm – 2 và 2 nằm về hai phía của điểm 0 và cách đều điểm 0.
c. Chỉ đúng với trường hợp những điểm nằm về bên phải điểm 0. Đối với những điểm nằm về bên trái điểm 0 thì ngược lại: điểm nào ở xa gốc hơn thì biểu diễn số nhỏ hơn.

a)
Người đó dừng lại tại điểm 5.
Kết quả của hai hành động trên: 2+3=5
b)
Người đó dừng lại tại điểm -5.
Tổng 2+3=5. Số đối của \(\left( {2 + 3} \right)\) là \( - 5\).
Vậy người đó dừng lại điểm cùng giá trị với số đối của tổng (2+3).

Khi biểu diễn trục số:
Số nhỏ hơn 0 thì biểu diễn bên trái điểm 0
Số lớn hơn 0 thì biểu diễn bên phải điểm 0
----------------------------------------------
A. \(-4< 0\) biểu diễn bên trái điểm 0
B. Đúng
C. \(2>0\) nên được biểu diễn bên phải điểm 0, không nằm giữa 0 và -2
D. \(-5< 0\) nên biểu diễn theo chiều âm

a)
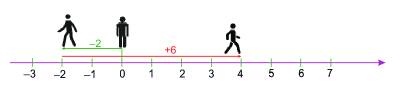
Người đó di chuyển về bên trái 2 đơn vị nên ta di chuyển sang trái 2 vạch (màu xanh) đến \( - 2\). Sau đó, sang phải 6 đơn vị nên ta di chuyển sang phải 6 vạch (màu đỏ) đến điểm +4. Vậy sau 2 lần di chuyển như trên, người đó dừng lại tại điểm +4.
Di chuyển sang trái 2 đơn vị là \(\left( { - 2} \right)\), sang phải 6 đơn vị là \(\left( { + 6} \right)\). Người đó dừng lại tại điểm +4 nên: \(\left( { - 2} \right) + \left( { + 6} \right) = + 4\).
b)
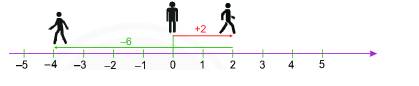
Người đó di chuyển về bên phải 2 đơn vị nên ta di chuyển sang phải 2 vạch. Sau đó, sang trái 6 đơn vị nên ta di chuyển sang trái 6 vạch đến điểm \( - 4\). Vậy sau 2 lần di chuyển như trên, người đó dừng lại tại điểm \( - 4\).
Di chuyển sang phải 2 đơn vị là \(\left( { + 2} \right)\), sang trái 6 đơn vị là \(\left( { - 6} \right)\). Người đó dừng lại tại điểm \( - 4\) nên: \(\left( { + 2} \right) + \left( { - 6} \right) = - 4\).

a) Người đó di chuyển về bên phải 4 đơn vị nên ta di chuyển sang phải 4 vạch. Sau đó, sang trái 4 đơn vị nên ta di chuyển sang trái 4 vạch đến điểm 0. Vậy sau 2 lần di chuyển như trên, người đó dừng lại tại điểm 0.
Di chuyển sang phải 4 đơn vị là \(\left( { + 4} \right)\), sang trái 4 đơn vị là \(\left( { - 4} \right)\). Người đó dừng lại tại điểm 0 nên: \(\left( { + 4} \right) + \left( { - 4} \right) = 0\)
b) Người đó di chuyển về bên trái 4 đơn vị nên ta di chuyển sang trái 4 vạch đến \( - 4\). Sau đó, sang phải 4 đơn vị nên ta di chuyển sang phải 4 vạch đến điểm 0. Vậy sau 2 lần di chuyển như trên, người đó dừng lại tại điểm 0.
Di chuyển sang trái 4 đơn vị là \(\left( { - 4} \right)\), sang phải 4 đơn vị là \(\left( { + 4} \right)\). Người đó dừng lại tại điểm 0 nên: \(\left( { - 4} \right) + \left( { + 4} \right) = 0\)





Tham khảo:
Bước 1. Vẽ đường thẳng nằm ngang có mũi tên như sau:
Bước 2. Trên đường thẳng đánh dấu các điểm cách đều nhau. Chọn một điểm ở giữa biểu diễn cho số 0.
Bước 3. Về bên phải số 0 biểu diễn các số tăng dần từ trái sang phải lần lượt là 1; 2; 3; …
- Biểu diễn số 1: Ta di chuyển 1 đơn vị về bên phải số 0.
- Biểu diễn số 2: Ta di chuyển 2 đơn vị về bên phải số 0.
- Biểu diễn tương tự với các số nguyên dương còn lại.
Về bên trái số 0 biểu diễn các số -1; -2; -3; …
- Biểu diễn số - 1: Ta di chuyển 1 đơn vị về bên trái số 0.
- Biểu diễn số - 2: Ta di chuyển 2 đơn vị về bên phải số 0.
- Biểu diễn tương tự với các số nguyên âm còn lại.