Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)
+) Số trung bình \(\overline x = \frac{{ - 2.10 + ( - 1).10 + 0.30 + 1.20 + 2.10}}{{10 + 20 + 30 + 20 + 10}} = 0\)
+) phương sai hoặc \({S^2} = \frac{1}{90}\left( {10.{{( - 2)}^2} + 10.{{( - 1)}^2} + ... + {{10.2}^2}} \right) - {0^2} = 4 \over 3\)
=> Độ lệch chuẩn \(S \approx 1,155\)
+) Khoảng biến thiên: \(R = 2 - ( - 2) = 4\)
Tứ phân vị: \({Q_2} = 0;{Q_1} = - 1;{Q_3} = 1\)
+) Khoảng tứ phân vị: \({\Delta _Q} = 1 - ( - 1) = 2\)
b) Giả sử cỡ mẫu \(n = 10\). Khi đó mẫu số liệu trở thành:
Giá trị | 0 | 1 | 2 | 3 | 4 |
Tần số | 1 | 2 | 4 | 2 | 1 |
+) Số trung bình \(\overline x = \frac{{0.0,1 + 1.0,2 + 2.0,4 + 3.0,2 + 4.0,1}}{{0,1 + 0,2 + 0,4 + 0,2 + 0,1}} = 2\)
+) phương sai hoặc \({S^2} = \frac{1}{1}\left( {0,{{1.0}^2} + 0,{{2.1}^2} + ... + 0,{{1.4}^2}} \right) - {2^2} = 1,2\)
=> Độ lệch chuẩn \(S \approx 1,1\)
+) Khoảng biến thiên: \(R = 4 - 0 = 4\)
Tứ phân vị: \({Q_2} = 2;{Q_1} = 1;{Q_3} = 3\)
+) Khoảng tứ phân vị: \({\Delta _Q} = 3 - 1 = 2\)

a)
+) Số trung bình \(\overline x = \frac{{6 + 8 + 3 + 4 + 5 + 6 + 7 + 2 + 4}}{9} = 5\)
+) phương sai hoặc \({S^2} = \frac{1}{9}\left( {{6^2} + {8^2} + ... + {4^2}} \right) - {5^2} = \frac{{10}}{3}\)
=> Độ lệch chuẩn \(S = \sqrt {\frac{{10}}{3}} \approx 1,8\)
Sắp xếp mẫu số liệu theo thứ tự không giảm: 2; 3; 4; 4; 5; 6; 6; 7; 8.
+) Khoảng biến thiên: \(R = 8 - 2 = 6\)
Tứ phân vị: \({Q_1},{Q_2},{Q_3}\)
\({Q_2} = {M_e} = 5\)
\({Q_1}\) là trung vị của nửa số liệu 2; 3; 4; 4. Do đó \({Q_1} = 3,5\)
\({Q_3}\) là trung vị của nửa số liệu: 6; 6; 7; 8. Do đó \({Q_3} = 6,5\)
+) Khoảng tứ phân vị: \({\Delta _Q} = 6,5 - 3,5 = 3\)
+) x là giá trị ngoại lệ trong mẫu nếu \(x > 6,5 + 1,5.3 = 11\) hoặc \(x < 3,5 - 1,5.3 = - 1\)
Vậy không có giá trị ngoại lệ trong mẫu số liệu trên.
b)
+) Số trung bình \(\overline x = \frac{{13 + 37 + 64 + 12 + 26 + 43 + 29 + 23}}{8} = 30,875\)
+) phương sai hoặc \({S^2} = \frac{1}{8}\left( {{{13}^2} + {{37}^2} + ... + {{23}^2}} \right) - 30,{875^2} \approx 255,8\)
=> Độ lệch chuẩn \(S \approx 16\)
Sắp xếp mẫu số liệu theo thứ tự không giảm: 12; 13; 23; 26; 29; 37; 43; 64.
+) Khoảng biến thiên: \(R = 64 - 12 = 52\)
Tứ phân vị: \({Q_1},{Q_2},{Q_3}\)
\({Q_2} = {M_e} = 27,5\)
\({Q_1}\) là trung vị của nửa số liệu 12; 13; 23; 26. Do đó \({Q_1} = 18\)
\({Q_3}\) là trung vị của nửa số liệu: 29; 37; 43; 64. Do đó \({Q_3} = 40\)
+) Khoảng tứ phân vị: \({\Delta _Q} = 40 - 18 = 22\)
+) x là giá trị ngoại lệ trong mẫu nếu \(x > 40 + 1,5.22 = 73\) hoặc \(x < 18 - 1,5.22 = - 15\)
Vậy không có giá trị ngoại lệ trong mẫu số liệu trên.

a) Xét mẫu số liệu đã sắp xếp là: \(2;2;5;7;10;10;13;15;19\)
Khoảng biến thiên của mẫu số liệu là: \(R = 19 - 2 = 17.\)
Cỡ mẫu là \(n = 9\) là số lẻ nên giá trị tứ phân vị thứ hai là: \({Q_2} = 10.\)
Tứ phân vị thứ nhất là trung vị của mẫu: \(2;2;5;7\). Do đó \({Q_1} = 3,5\)
Tứ phân vị thứ ba là trung vị của mẫu: \(10;13;15;19\). Do đó \({Q_3} = 14\)
Khoảng tứ phân vị của mẫu là: \({\Delta _Q} = 14 - 3,5 = 10,5\)
b) Xét mẫu số liệu đã sắp xếp là: \(1;2;5;5;9;10;10;15;15;19\)
Khoảng biến thiên của mẫu số liệu là: \(R = 19 - 1 = 18.\)
Cỡ mẫu là \(n = 10\) là số chẵn nên giá trị tứ phân vị thứ hai là: \({Q_2} = 9,5.\)
Tứ phân vị thứ nhất là trung vị của mẫu: \(1;2;5;5;9\). Do đó \({Q_1} = 5.\)
Tứ phân vị thứ ba là trung vị của mẫu: \(10;10;15;15;19\). Do đó \({Q_3} = 15\)
Khoảng tứ phân vị của mẫu là: \({\Delta _Q} = 15 - 5 = 10\)

Tham khảo:
n=10
Giả sử sau khi sắp xếp 10 số dương theo thứ tự không giảm thì được:

=> Trung vị là giá trị trung bình của số thứ 5 và thứ 6.
=> \({Q_1}\) là số thứ 3 và \({Q_3}\) là số thứ 8.
a) Khi nhân mỗi giá trị của mẫu số liệu với 2 thì:
+ Số lớn nhất tăng 2 lần và số nhỏ nhất tăng 2 lần
=> R tăng 2 lần
+ \({Q_1}\) và \({Q_3}\) tăng 2 lần
=> Khoảng tứ phân vị \({\Delta _Q} = {Q_3} - {Q_1}\) tăng 2 lần.
+ Giá trị trung bình tăng 2 lần
=> Độ lệch của mỗi giá trị so với giá trị trung bình \(\left| {{x_i} - \overline x} \right|\) cũng tăng 2 lần
=> \({\left( {{x_i} - \overline x} \right)^2}\) tăng 4 lần
=> Phương sai tăng 4 lần
=> Độ lệch chuẩn tăng 2 lần.
Vậy R tăng 2 lần, khoảng tứ phân vị tăng 2 lần và độ lệch chuẩn tăng 2 lần.
b) Cộng mỗi giá trị của mẫu số liệu với 2 thì
+ Số lớn nhất tăng 2 đơn vị và số nhỏ nhất tăng 2 đơn vị
=> R không đổi vì phần tăng thêm bị triệt tiêu cho nhau.
+ \({Q_1}\) và \({Q_3}\) tăng 2 đơn vị
=> Khoảng tứ phân vị \({\Delta _Q} = {Q_3} - {Q_1}\) không đổi vì phần tăng thêm bị triệt tiêu cho nhau.
+ Giá trị trung bình tăng 2 đơn vị
=> Độ lệch của mỗi giá trị so với giá trị trung bình \(\left| {{x_i} - \overline x} \right|\) không đổi vì phần tăng thêm bị triệt tiêu cho nhau.
=> \({\left( {{x_i} - \overline x} \right)^2}\) không đổi
=> Phương sai không đổi.
=> Độ lệch chuẩn không đổi.
Vậy khoảng biến thiên, khoảng tứ phân vị và độ lệch chuẩn đều không đổi.

a)
Số trung bình \(\overline x = \frac{{8.1 + 19.10 + 20.19 + 21.17 + 22.3}}{{1 + 10 + 19 + 17 + 3}} = 20,02\)
+) Sắp xếp các giá trị theo thứ tự không giảm: \(8,\underbrace {19,...,19}_{10},\underbrace {20,...,20}_{19},\underbrace {21,...,21}_{17},22,22,22\)
Trung vị \({M_e} = \frac{1}{2}(20 + 20) = 20\)
+) Mốt \({M_o} = 20\)
b)
+) Tình độ lệch chuẩn:
Phương sai \({S^2} = \frac{1}{{50}}\left( {{8^2} + {{10.19}^2} + {{19.20}^2} + {{17.21}^2} + {{3.22}^2}} \right) - 20,{02^2} \approx 3,66\)
=> Độ lệch chuẩn \(S = \sqrt {{S^2}} \approx 1,91\)
+) Khoảng biến thiên \(R = 22 - 8 = 14\)
+) Tứ phân vị: \({Q_1},{Q_2},{Q_3}\)
\({Q_2} = {M_e} = 20\)
\({Q_1}\) là trung vị của mẫu: \(8,\underbrace {19,...,19}_{10},\underbrace {20,...,20}_{14}\). Do đó \({Q_1} = 20\)
\({Q_3}\) là trung vị của mẫu: \(\underbrace {20,...,20}_5,\underbrace {21,...,21}_{17},22,22,22\). Do đó \({Q_3} = 21\)
+) x là giá trị ngoại lệ nếu \(x > 21 + 1,5(21 - 20) = 22,5\) hoặc \(x < 20 - 1,5.(21 - 10) = 18,5\).
Vậy có một giá trị ngoại lệ là 8.

Sắp xếp theo thứ tự không giảm.
2,593 2,977 3,155 3,270 3,387 3,412 3,813 3,920 4,042 4,236
Khoảng biến thiên \(R = 4,236 - 2,593 = 1,643\)
Vì n=10 nên ta có:
\({Q_1} = 3,155\); \({Q_3} = 3,920\)
Khoảng tứ phân vị \({\Delta _Q} = {Q_3} - {Q_1} = 3,920 - 3,155\)\( = 0,765\)
\(\overline x \approx 3,481\)
Ta có:
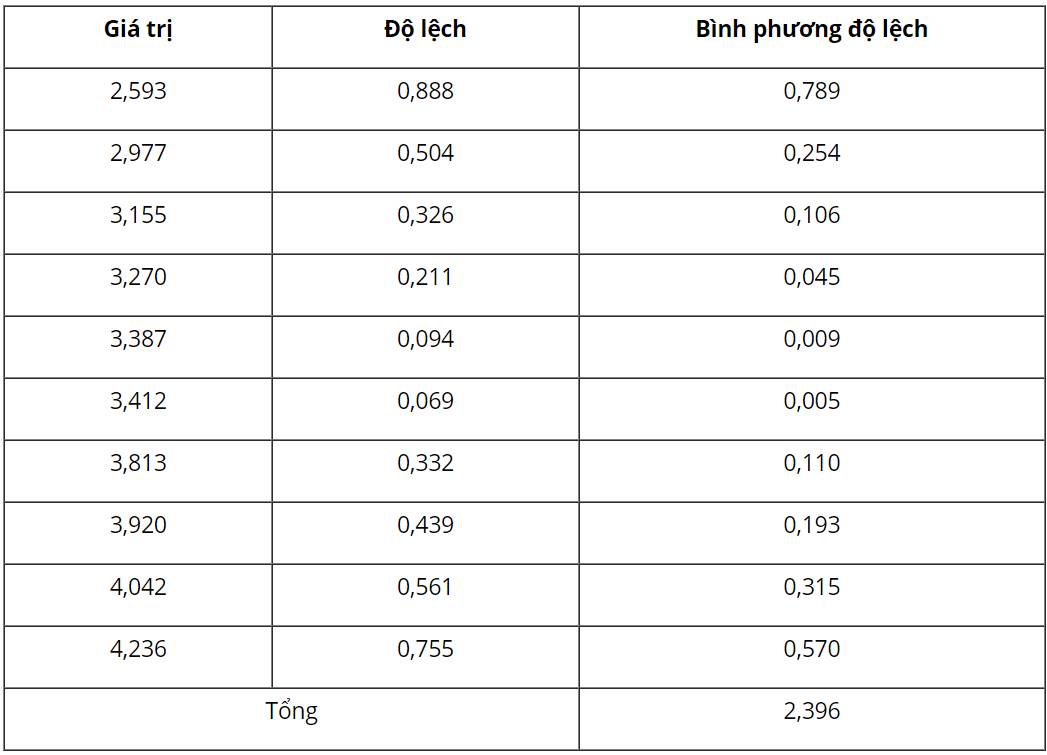
Độ lệch chuẩn: \(s = \sqrt {0,2396} \approx 0,489\)Phương sai là: \({s_2} = \frac{{2,396}}{{10}} = 0,2396\)

Câu 3:
Theo đề, ta có;
\(\left\{{}\begin{matrix}4a+2b+c=3\\-\dfrac{b}{2a}=1\\-\dfrac{b^2-4ac}{4a}=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=-2a\\b^2-4ac=-8a\\4a+2b+c=3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}b=-2a\\4a^2-4ac=-8a\\4a+2b+c=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=-2a\\4a\left(a-c\right)=4a\cdot\left(-2\right)\\4a+2b+c=3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}b=-2a\\c=a+2\\4a-4a+a+2=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=1\\b=-2\\c=3\end{matrix}\right.\)
Câu 3:
Theo đề, ta có;
\(\left\{{}\begin{matrix}4a+2b+c=3\\-\dfrac{b}{2a}=1\\-\dfrac{b^2-4ac}{4a}=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=-2a\\b^2-4ac=-8a\\4a+2b+c=3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}b=-2a\\4a^2-4ac=-8a\\4a+2b+c=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=-2a\\4a\left(a-c\right)=4a\cdot\left(-2\right)\\4a+2b+c=3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}b=-2a\\c=a+2\\4a-4a+a+2=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=1\\b=-2\\c=3\end{matrix}\right.\)

a) Số trung bình cộng của mẫu số liệu trên là: \(\overline X = \frac{{165 + 155 + 171 + 167 + 159 + 175 + 165 + 160 + 158}}{9} = 163,9\)
b) Mẫu số liệu theo thứ tự không giảm là:
155 158 159 160 165 165 167 171 175
Mẫu số liệu trên có 9 số liệu nên số trung vị là: \({M_e} = 165\)
c) Ta có bàng tần số
155 | 158 | 159 | 160 | 165 | 167 | 171 | 175 |
1 | 1 | 1 | 1 | 2 | 1 | 1 | 1 |
Vậy mốt của mẫu số liệu là: \({M_o} = 165\)
d) Mẫu số liệu theo thứ tự không giảm là:
155 158 159 160 165 165 167 171 175
Mẫu số liệu trên có 9 số liệu nên số trung vị là: \({M_e} = 165\)
Trung vi của dãy số 155 158 159 160 là: \({Q_1} = \frac{{158 + 159}}{2} = 158,5\)
Trung vị của dãy số 165 167 171 175 là: \({Q_3} = \frac{{167 + 171}}{2} = 169\)
Vậy \({Q_1} = 158,5\), \({Q_2} = 165\), \({Q_3} = 169\)
Ví dụ, ta có bảng đo chiều cao của các bạn trong tổ như sau:
160
162
164
165
172
174
177
178
180
a) Sắp xếp mẫu số liệu theo thứ tự không giảm ta được:
160 162 164 165 172 174 177 178 180
Số trung bình cộng của mẫu số liệu trên là:
\(\overline x = \frac{{160\;\; + 162\;\; + 164\;\;\; + \;\;165\;\; + \;172\;\; + \;174\;\; + \;177\; + \;\;178\; + \;180}}{9} = \frac{{1532}}{9}\)
Trung vị của mẫu số liệu trên là: Do mẫu số liệu trên có 9 số liệu ( lẻ ) nên trung vị \({Q_2} = 172\)
Tứ phân vị của mẫu số liệu trên là:
- Trung vị của dãy 160 162 164 165 là: \({Q_1} = 163\)
- Trung vị của dãy 174 177 178 180 là: \({Q_3} = 177,5\)
- Vậy tứ phân vị của mẫu số liệu là: \({Q_1} = 163\), \({Q_2} = 172\), \({Q_3} = 177,5\)
b) Khoảng biến thiên của mẫu số liệu trên là: \(R = {x_{\max }} - {x_{\min }} = 180 - 160 = 20\)
Khoảng tứ phân vị của mẫu số liệu trên là: \({\Delta _Q} = {Q_3} - {Q_1} = 177,5 - 163 = 14,5\)
c) Phương sai của mẫu số liệu trên là:
\({s^2} = \frac{{\left[ {{{\left( {160 - \overline x } \right)}^2} + {{\left( {162 - \overline x } \right)}^2} + ... + {{\left( {180 - \overline x } \right)}^2}} \right]}}{9} \approx 50,84\)
Độ lệch chuẩn của mẫu số liệu trên là: \(s = \sqrt {{s^2}} \approx 7,13\)