Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Quy tắc cộng hai số nguyên cùng mẫu:
Ta lấy tử số cộng với nhau và giữ nguyên mẫu số.
+) \(\dfrac{8}{{11}} + \dfrac{3}{{11}} = \dfrac{{8 + 3}}{{11}} = \dfrac{{11}}{{11}} = 1\)
+) \(\dfrac{9}{{12}} + \dfrac{{11}}{{12}} = \dfrac{{9 + 11}}{{12}} = \dfrac{{20}}{{12}}\)\( = \dfrac{{20:4}}{{12:4}} = \dfrac{5}{3}\)

* Quy tắc trừ hai phân số cùng mẫu: Muốn trừ 2 phân số có cùng mẫu số, ta lấy tử số của phân số thứ nhất trừ đi tử số của phân số thứ hai và giữ nguyên mẫu.
* Ta có: \(\dfrac{7}{{13}} - \dfrac{5}{{13}} = \dfrac{{7 - 5}}{{13}} = \dfrac{2}{{13}}\) và \(\dfrac{3}{4} - \dfrac{1}{5} = \dfrac{{15}}{{20}} - \dfrac{4}{{20}} = \dfrac{{15 - 4}}{{20}} = \dfrac{{11}}{{20}}\)

* Quy tắc chia hai phân số có tử mẫu đều dương: Lấy số bị chia nhân với phân số nghịch đảo của số chia.
\(\dfrac{3}{4}:\dfrac{2}{5} = \dfrac{3}{4}.\dfrac{5}{2} = \dfrac{{3.5}}{{4.2}} = \dfrac{{15}}{8}\)

* Quy tắc nhân 2 phân số: Nhân tử với tử, mẫu với mẫu.
\(\dfrac{8}{3}.\dfrac{3}{7} = \dfrac{{8.3}}{{3.7}} = \dfrac{{24}}{{21}} = \dfrac{{24:3}}{{21:3}} = \dfrac{8}{7}\)
\(\dfrac{4}{6}.\dfrac{5}{8} = \dfrac{{4.5}}{{6.8}} = \dfrac{{20}}{{48}} = \dfrac{{20:4}}{{48:4}} = \dfrac{5}{{12}}\)

+ Quy đồng mẫu các phân số: \(\dfrac{3}{4}\) và \(\dfrac{5}{6}\):
\(BCNN\left( {6,4} \right) = 12\)
Thừa số phụ: \(12:4 = 3; 12:6=2\)
Ta có: \(\dfrac{3}{4} = \dfrac{{3.3}}{{4.3}} = \dfrac{9}{{12}}\\\dfrac{5}{6} = \dfrac{{5.2}}{{6.2}} = \dfrac{{10}}{{12}}\)
+ So sánh hai phân số cùng mẫu:
Vì 9 < 10 nên \(\dfrac{9}{{12}} < \dfrac{{10}}{{12}}\) nên \(\dfrac{3}{4} < \dfrac{5}{6}\).

Ta có: \(\dfrac{5}{7} = \dfrac{{5.4}}{{7.4}} = \dfrac{{20}}{{28}}\) và \(\dfrac{{ - 3}}{4} = \dfrac{{ - 3.7}}{{4.7}} = \dfrac{{ - 21}}{{28}}\)
Như vậy, \(\dfrac{{20}}{{28}} + \dfrac{{ - 21}}{{28}} = \dfrac{{20 + \left( { - 21} \right)}}{{28}} = \dfrac{-1}{{28}}\)

![]() hai phân số có cùng tử thì so sánh mẫu .
hai phân số có cùng tử thì so sánh mẫu .
![]() hai phân số mà có cùng mẫu thì so sánh tử .Hết
hai phân số mà có cùng mẫu thì so sánh tử .Hết
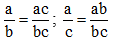
Quy tắc:
Trong hai phân số có cùng mẫu, phân số nào có tử lớn hơn thì lớn hơn.
So sánh:
Ta có 7 < 9 nên \(\dfrac{7}{{11}} < \dfrac{9}{{11}}\).