LN
6
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
S
7
TL
14 tháng 8
cô Hoài có khá nhiều việc nên cô từ từ mới thấy tin nhắn của bạn nhé
13 tháng 2 2022
-Vì bài dài quá nên mình nói tóm tắt:
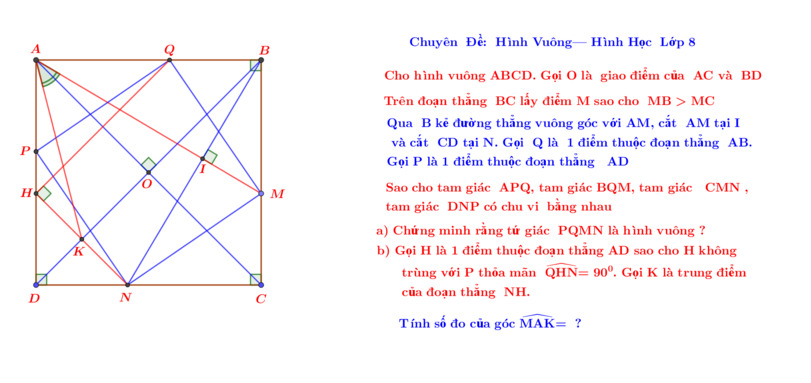
a) -Bạn chứng minh △ABM = △BCN (g-c-g) do có \(AB=BC\) , \(\widehat{BCN}=\widehat{ABM}=90^0\),\(\widehat{NBC}=\widehat{MAB}\) (bạn tự chứng minh).
-Suy ra: \(BM=CN\) .
-Suy ra 2 điều:
+\(QM^2-BQ^2=MN^2-MC^2\)
+\(QM+BQ=MN+MC\) (1)
\(QM^2-BQ^2=MN^2-MC^2\)
\(\Rightarrow\left(QM-BQ\right)\left(QM+BQ\right)=\left(MN-MC\right)\left(MN+MC\right)\)
\(\Rightarrow QM-BQ=MN-MC\) (2)
-Từ (1),(2) suy ra \(QM=MN\) nên △BMQ=△CNM (ch-cgv).
\(\Rightarrow\) MQ vuông góc với MN (bạn tự c/m).
\(QM=MN\) nên \(BQ=MC\) nên \(AQ=BM\Rightarrow PQ^2-AP^2=QM^2-BQ^2;QM+BQ=PQ+AP\)
Nên \(PQ=QM;\Delta APQ=\Delta BQM\) nên PQ⊥QM ; AP=BQ nên PQ=AQ
-Từ PQ=AQ bạn tự c/m PN=PQ (theo sườn mình đã cho) rồi sau đó c/m tam giác APQ=tam giác DNP rồi từ đó suy ra PQ vuông góc PN
.......
PK
0
13 tháng 9 2020
Dung à mày (:
Ta có \(\frac{1}{\left(x+1\right)^2\left(x+2\right)}=\frac{a}{x+1}+\frac{b}{\left(x+1\right)^2}+\frac{c}{x+2}\)
\(\Leftrightarrow\frac{1}{\left(x+1\right)^2\left(x+2\right)}=\frac{a\left(x+1\right)\left(x+2\right)}{\left(x+1\right)^2\left(x+2\right)}+\frac{b\left(x+2\right)}{\left(x+1\right)^2\left(x+2\right)}+\frac{c\left(x+1\right)^2}{\left(x+1\right)^2\left(x+2\right)}\)
\(\Leftrightarrow\frac{1}{\left(x+1\right)^2\left(x+2\right)}=\frac{a\left(x^2+3x+2\right)}{\left(x+1\right)^2\left(x+2\right)}+\frac{bx+2b}{\left(x+1\right)^2\left(x+2\right)}+\frac{c\left(x^2+2x+1\right)}{\left(x+1\right)^2\left(x+2\right)}\)
\(\Leftrightarrow\frac{1}{\left(x+1\right)^2\left(x+2\right)}=\frac{ax^2+3ax+2a+bx+2b+cx^2+2cx+c}{\left(x+1\right)^2\left(x+2\right)}\)
\(\Leftrightarrow\frac{1}{\left(x+1\right)^2\left(x+2\right)}=\frac{x^2\left(a+c\right)+x\left(3a+b+2c\right)+\left(2a+2b+c\right)}{\left(x+1\right)^2\left(x+2\right)}\)
\(\Rightarrow1=x^2\left(a+c\right)+x\left(3a+b+2c\right)+\left(2a+2b+c\right)\)
Đồng nhất hệ số ta được :
\(\hept{\begin{cases}a+c=0\\3a+b+2c=0\\2a+2b+c=1\end{cases}}\)=> Chịu :)) Khó quá không làm được ... Hoặc do đề sai ;-;
13 tháng 9 2020
Không sai == Trong sách Nâng cao và phát triển toán 8 tập 1 trang 33 bài 123 ý c
T cũng chịu '-'
12 tháng 10 2020
Sao lạ thế nhỉ, áp cái được luôn?
\(2a+\frac{b}{a}+\frac{c}{b}\ge3\sqrt[3]{2a.\frac{b}{a}.\frac{c}{b}}=3\sqrt[3]{2c}\)
Đẳng thức tự xét.
bạn đăng lại câu hỏi của bạn nhé, câu hỏi của bạn bị lỗi rồi
câu j