
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
OZ
0

Các câu hỏi dưới đây có thể giống với câu hỏi trên
HM
0

FN
0


19 tháng 3 2017
Ban đầu, vật trung hòa về điện. (có tổng điện tích âm của electron có trị số tuyệt đối bằng điện tích dương của hạt nhân)
Trong khi cọ xát; electron được chuyển từ vật này sang vật khác => không còn trung hòa về điện nữa (tổng điện tích âm của các electron có trị số tuyệt đối không bằng điện tích dương của hạt nhân) =>vật nhiễm điện


20 tháng 4 2017
4λ=20,45−12,42=4,0254λ=20,45−12,42=4,025cm => λ = 1,006cm ≈ 0,01m.
Vậy v = λ.f = 0,01.50 = 0,5m/s.




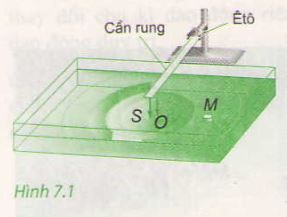
 thầy có thể giảng cho em câu 7 trong đề đc k ạ . Em cảm ơn
thầy có thể giảng cho em câu 7 trong đề đc k ạ . Em cảm ơn